SCHEME OF WORK
WEEK TOPIC
1. Revision of last year's work.
2. Number Bases: Conversion from and to Denary, Binary numbers: The concept of Binary number system, Arithmetical operations in Binary system, Conversion of numbers in Binary to other bases and vice versa.
3. Use of Mathematics in ICT. Using Computer to do simple Mathematical calculations. Translation of word problems into numerical expressions.
4.Whole numbers (cont’d): Expressions involving brackets and fractions. Solving problems involving direct and inverse proportions. Application of direct and inverse proportions to practical problems (convert word problems to numerical expressions and solve).
5. Compound Interest. Solving problems on Compound Interest and the use of Compound Interest in daily life. Decimal Places and Significant Figures. Solve Quantitative Reasoning problems. The concept of Pi (π).
6. Conversion of base 10 numerals to Binary numbers: Converting numbers between 1-10 to base 2. Solving problems on Quantitative Reasoning, using conversion of numerals from base 10 to base 2.
7. Computer applications: Use of Punched Cards to store information. Writing familiar words in Coded form.
8. Factorization: Factorization of expressions of the form: ax+ay,3m+pq+3p+mp,a2-b2, a2-2ab+b2. Word problems involving factorization.
9. Area and volume of cylinders and cones (Revision)
10. Reading tabulated Data. Charts and tables. Graph of social environmental issues.
11. Profit & Loss. Percentage profit or loss. Finding Cost Price & Selling Price
12. Simultaneous Equations (Substitution Method).
13. REVISION TOPICS - Factorization (Common Factors).
14. REVISION TOPICS - Factorization of Quadratic Expression.
15. REVISION TOPICS - Factorization (Removing Brackets.
16. REVISION TOPICS - Substitution and change of subject.
17. REVISION TOPICS - Solving equations involving fractions. Word Problems involving Fractions
18. REVISION TOPICS - Similarity (Identification and properties of similar shapes). Area of similar shapes. Volume of similar shapes.
19. GENERAL REVISION
1ST TERM
WEEK 1
TOPIC: NUMBER BASES
CONTENT:
Concept and types of number base.
Binary numbers.
Conversion in number bases: Denary to Binary, Binary to Denary, Denary to other bases, One base to another, etc.
Arithmetical operation in Binary System: Addition, Subtraction, Multiplication and Division.
Bicimal numbers: Conversion, Addition and Subtraction.
Equation in number bases.
Quantative Aptitude Reasons (QAR) on number bases.
LESSON 1
CONCEPT AND TYPES OF NUMBER BASES
Number Base is a system of counting natural numbers in bunddles. Some language have their own unique method or way of counting numbers while others have same method. For instance, numbers are counted in bundle of ten digits called base ten or denary. The digits in involve in English natural numbers are: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Some unique number bases include: Base 2 ( Binary), Base 8 (Octal), Base 10 (Denary or Decimal), Base 16 (Hexadecimal),… there are other bases such as base 3, base 4, base 5, base 6, etc. The bases of number system are usually written as a
subscript either in word or figure. Examples: 1110112 or 111011two, 57348 or
5734eight, 78110 or 781ten, etc.
NOTE: Numbers in base ten can be written without the base indicated. Therefore any number base that is written without base indicated should be considered as denary or base ten numbers.
https://www.youtube.com/watch?v=L2zsmYaI5ww
CLASS ACTIVITY:
Students to count in their mother tongues.
LESSON 2
BINARY NUMBERS.
Binary numbers are system of counting numbers in base two. In binary system , the greatest digit is 1 and the least or lowest is 0. Hence, the two digits available in binary numbers are 1 and 0. Binary numbers is the most important number bases
because of its usage in computer. Examples of binary numbers are 111112, 1000001two,
01012, etc.
https://www.youtube.com/watch?v=LpuPe81bc2w
LESSON 3
EXPRESSING BINARY AS SUM OF MULTIPLES
We can easily express any binary number as power of multiples of two as shown in the following examples.
110two =(1×22)+(1×21)+(0×20)
11112 =(1×23)+(1×22)+(1×21) (1×20)
10001tw0=(1×24)+(0×23)+(0×22)+(0×21)+(1×20)
https://www.youtube.com/watch?v=hIs3A6gGz2w
EVALUATION:
Express each of the following as multiples of power of its base
(1) 1011two
(2) 11000110two
(3) 832ten
(4) 890.701ten
(5) 100.1001two
(6) 4302.42six
(7) 0.0247eight
LESSON 4
CONVERSION OF BINARY NUMBERS TO DECIMAL NUMBERS
To express binary numbers in decimals or denaries, we write the binary number as a sum of multiples of powers of two, or we multiply each digit by the base and add to the next digit starting from the left.
NOTE: Any number or letter raised to the power of zero is 1
Examples:
Convert 1111two to denary scale.
Solution:
1111two =(1×23)+(1×22)+(1×21) (1×20)
=8+4+2+1=15ten.
Express 11101two to decimal number
Solution:
11101two =(1×24)+(1×23)+(1×22)+(0×21)+(1×20)
=16+8+4+0+1=29ten
Convert 1111110two to a number in base ten.
Solution:
1111110two =(1×26)+(1×25)+(1×24)+(1×23)+(1×22)
(1×21)+(0×20)
=64+32+16+8+4+2+0=126ten
https://www.youtube.com/watch?v=VLflTjd3lWA
EVALUATION:
Express the following binary numbers to denary.
110111two
2. 1010101010two
3. 10000000101two

LESSON 5
CONVERSION OF OTHER NUMBER BASES TO DENARY
Converting other number bases to denary is the same as that of binary discussed earlier. Lets study the examples below.
Express 56eight to denary
Solution:
56eight =(5×81)+(6×80)=40+6=46ten
Convert 1243five to base ten
Solution:
1243five =(1×53)+(2×52)+(4×51) (3×50)
=125+50+20+3=198ten
https://www.youtube.com/watch?v=q7nZbAUTSC4
EVALUATION:
Express in denary the following number bases:
124eight 2. 25seven 3. 48nine 4. 211five

CONVERSION FROM DENARY TO ANY BASE
In converting a denary number to base two (binary) or any other base, we divide by that new base keeping the remainder in each step until there is nothing more to divide. The result is the list of remainders from the last to the first.
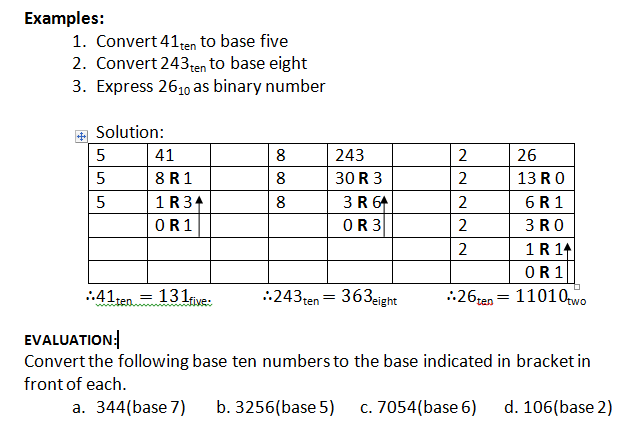
https://www.youtube.com/watch?v=zhpNjG_a-kc
CONVERTING FROM ONE BASE TO ANOTHER BASE OTHER THAN BASE 10
To do this, two steps are involved:
Step1: convert the given base to base ten.
Step2: convert the result gotten from step1 above to the required base.

https://www.youtube.com/watch?v=6ts6JtSBSu8
EVALUATION:
Convert: (a) 4056 to binary (b) 3214 to octal scale (c) 6548 to base three.
LESSON 6
BICIMAL NUMBERS.
decimals are binary numbers in fractional form in which the denominator is a power of 2. Examples includes 10.1012, 0.1112, 1011.11012, etc.
https://www.youtube.com/watch?v=_jcW-ZgpRbM
https://www.youtube.com/watch?v=3FA8yQ0cZyE
CONVERSION OF BICIMAL TO DENARY
In converting bicimal numbers to denary, we write the bicimal numbers as a sum of multiples of powers of two. The whole numbers parts of bicimal are raised to positive power of 2 increasing to the left starting with zero. While the fractional part are raised to negative power of 2 decreasing to the left starting with negative 1(-1).

NOTE: Other bases in fractional form other than bicimal can also be expressed in denary using the same method as in bicimal. https://www.youtube.com/watch?v=OezK_zTyvAQ
EVALUATION:
Convert each of the following to denary scale.
10112 b. 32568 c. 101.1012 d. 43.218 e. 32.215 f. 5329.
LESSON 7
: ARITHMETIC OPERATIONS IN NUMBER
Basic operations of addition, subtraction, multiplication and division are carried out in other bases exactly the same as base 10.
ADDITION IN BINARY SYSTEM
To add in binary number, the following steps are important:
Arrange the numbers as in the addition of decimal numbers.
Add the elements of the column starting with the right most column.
Divide the sum by two.
Record the remainder, which is either 0 or 1.
Add the quotient to the sum of the next column and repeat the process for the next column.
https://www.youtube.com/watch?v=5F6orbqZigI

ADDITION IN OTHER BASES:
The same principle applied when performing addition in binary and denary is applicable here also.
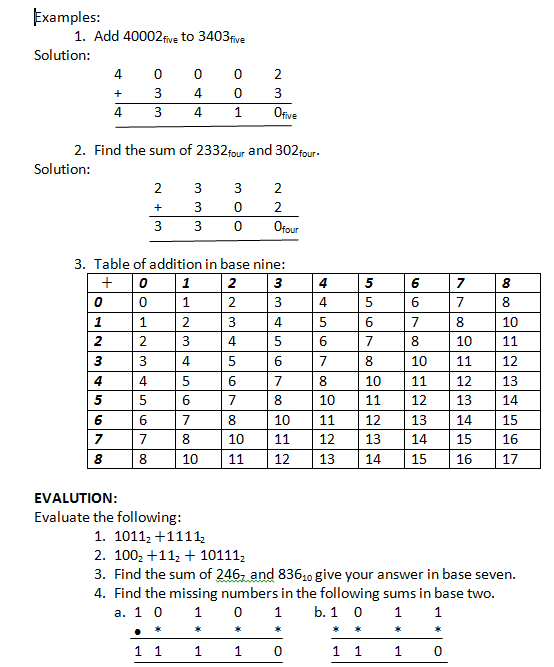
https://www.youtube.com/watch?v=yDh1_pLrbJY
SUBTRACTION IN BASE TWO AND OTHER BASES
Subtraction in binary numbers are the same as subtraction in denary numbers. When the digit of the number to be subtracted is larger than the corresponding digit above it, we transfer one 2 from the next left column. If the immediate next column has zero digit, the transfer will be from further left column. The same principle is applicable to other bases other than base 2.

https://www.youtube.com/watch?v=hZj9yfMa130
LESSON 8
MULTIPLICATION AND DIVISION OF NUMBER BASES
MULTIPLICATION is a repeated addition. This principle is always applied while multiplying binary numbers and other number bases. The important thing we must note is that if we are working in base two and other bases, all the figures we use in the working should be less than 2 or the number base under consideration.
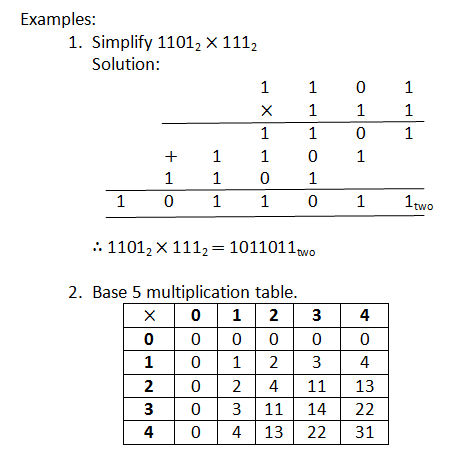
https://www.youtube.com/watch?v=k6nO3EGVhfw
DIVISION in base two is very similar to division in base ten. If the two numbers are in the same base, we divide using the long division method. However, if both numbers are not in the same base, we convert to base ten and then to the base required before solving.

https://www.youtube.com/watch?v=JYTHm7HBInQ
ASSIGNMENT
Nelson Functional Mathematics for JSS Book3, Graduated Exercises Page 24-25,Qustions 4, 26-35.
Nelson Functional Mathematical for JSS WorkBook3, Page 2-3,Qustions d and e
Read...
Nelson functional Mathematics for JSS Book3, Page 1-25.
New General Mathematics for JSS3 UBE Edition, Page 14-22.
Nelson functional Mathematics for JSS WorkBook3, Page 1-7.
CONTENT:
Concept and types of number base.
Binary numbers.
Conversion in number bases: Denary to Binary, Binary to Denary, Denary to other bases, One base to another, etc.
Arithmetical operation in Binary System: Addition, Subtraction, Multiplication and Division.
Bicimal numbers: Conversion, Addition and Subtraction.
Equation in number bases.
Quantative Aptitude Reasons (QAR) on number bases.
LESSON 1
CONCEPT AND TYPES OF NUMBER BASES
Number Base is a system of counting natural numbers in bunddles. Some language have their own unique method or way of counting numbers while others have same method. For instance, numbers are counted in bundle of ten digits called base ten or denary. The digits in involve in English natural numbers are: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Some unique number bases include: Base 2 ( Binary), Base 8 (Octal), Base 10 (Denary or Decimal), Base 16 (Hexadecimal),… there are other bases such as base 3, base 4, base 5, base 6, etc. The bases of number system are usually written as a
subscript either in word or figure. Examples: 1110112 or 111011two, 57348 or
5734eight, 78110 or 781ten, etc.
NOTE: Numbers in base ten can be written without the base indicated. Therefore any number base that is written without base indicated should be considered as denary or base ten numbers.
https://www.youtube.com/watch?v=L2zsmYaI5ww
CLASS ACTIVITY:
Students to count in their mother tongues.
LESSON 2
BINARY NUMBERS.
Binary numbers are system of counting numbers in base two. In binary system , the greatest digit is 1 and the least or lowest is 0. Hence, the two digits available in binary numbers are 1 and 0. Binary numbers is the most important number bases
because of its usage in computer. Examples of binary numbers are 111112, 1000001two,
01012, etc.
https://www.youtube.com/watch?v=LpuPe81bc2w
LESSON 3
EXPRESSING BINARY AS SUM OF MULTIPLES
We can easily express any binary number as power of multiples of two as shown in the following examples.
110two =(1×22)+(1×21)+(0×20)
11112 =(1×23)+(1×22)+(1×21) (1×20)
10001tw0=(1×24)+(0×23)+(0×22)+(0×21)+(1×20)
https://www.youtube.com/watch?v=hIs3A6gGz2w
EVALUATION:
Express each of the following as multiples of power of its base
(1) 1011two
(2) 11000110two
(3) 832ten
(4) 890.701ten
(5) 100.1001two
(6) 4302.42six
(7) 0.0247eight
LESSON 4
CONVERSION OF BINARY NUMBERS TO DECIMAL NUMBERS
To express binary numbers in decimals or denaries, we write the binary number as a sum of multiples of powers of two, or we multiply each digit by the base and add to the next digit starting from the left.
NOTE: Any number or letter raised to the power of zero is 1
Examples:
Convert 1111two to denary scale.
Solution:
1111two =(1×23)+(1×22)+(1×21) (1×20)
=8+4+2+1=15ten.
Express 11101two to decimal number
Solution:
11101two =(1×24)+(1×23)+(1×22)+(0×21)+(1×20)
=16+8+4+0+1=29ten
Convert 1111110two to a number in base ten.
Solution:
1111110two =(1×26)+(1×25)+(1×24)+(1×23)+(1×22)
(1×21)+(0×20)
=64+32+16+8+4+2+0=126ten
https://www.youtube.com/watch?v=VLflTjd3lWA
EVALUATION:
Express the following binary numbers to denary.
110111two
2. 1010101010two
3. 10000000101two

LESSON 5
CONVERSION OF OTHER NUMBER BASES TO DENARY
Converting other number bases to denary is the same as that of binary discussed earlier. Lets study the examples below.
Express 56eight to denary
Solution:
56eight =(5×81)+(6×80)=40+6=46ten
Convert 1243five to base ten
Solution:
1243five =(1×53)+(2×52)+(4×51) (3×50)
=125+50+20+3=198ten
https://www.youtube.com/watch?v=q7nZbAUTSC4
EVALUATION:
Express in denary the following number bases:
124eight 2. 25seven 3. 48nine 4. 211five

CONVERSION FROM DENARY TO ANY BASE
In converting a denary number to base two (binary) or any other base, we divide by that new base keeping the remainder in each step until there is nothing more to divide. The result is the list of remainders from the last to the first.

https://www.youtube.com/watch?v=zhpNjG_a-kc
CONVERTING FROM ONE BASE TO ANOTHER BASE OTHER THAN BASE 10
To do this, two steps are involved:
Step1: convert the given base to base ten.
Step2: convert the result gotten from step1 above to the required base.

https://www.youtube.com/watch?v=6ts6JtSBSu8
EVALUATION:
Convert: (a) 4056 to binary (b) 3214 to octal scale (c) 6548 to base three.
LESSON 6
BICIMAL NUMBERS.
decimals are binary numbers in fractional form in which the denominator is a power of 2. Examples includes 10.1012, 0.1112, 1011.11012, etc.
https://www.youtube.com/watch?v=_jcW-ZgpRbM
https://www.youtube.com/watch?v=3FA8yQ0cZyE
CONVERSION OF BICIMAL TO DENARY
In converting bicimal numbers to denary, we write the bicimal numbers as a sum of multiples of powers of two. The whole numbers parts of bicimal are raised to positive power of 2 increasing to the left starting with zero. While the fractional part are raised to negative power of 2 decreasing to the left starting with negative 1(-1).

NOTE: Other bases in fractional form other than bicimal can also be expressed in denary using the same method as in bicimal. https://www.youtube.com/watch?v=OezK_zTyvAQ
EVALUATION:
Convert each of the following to denary scale.
10112 b. 32568 c. 101.1012 d. 43.218 e. 32.215 f. 5329.
LESSON 7
: ARITHMETIC OPERATIONS IN NUMBER
Basic operations of addition, subtraction, multiplication and division are carried out in other bases exactly the same as base 10.
ADDITION IN BINARY SYSTEM
To add in binary number, the following steps are important:
Arrange the numbers as in the addition of decimal numbers.
Add the elements of the column starting with the right most column.
Divide the sum by two.
Record the remainder, which is either 0 or 1.
Add the quotient to the sum of the next column and repeat the process for the next column.
https://www.youtube.com/watch?v=5F6orbqZigI

ADDITION IN OTHER BASES:
The same principle applied when performing addition in binary and denary is applicable here also.

https://www.youtube.com/watch?v=yDh1_pLrbJY
SUBTRACTION IN BASE TWO AND OTHER BASES
Subtraction in binary numbers are the same as subtraction in denary numbers. When the digit of the number to be subtracted is larger than the corresponding digit above it, we transfer one 2 from the next left column. If the immediate next column has zero digit, the transfer will be from further left column. The same principle is applicable to other bases other than base 2.

https://www.youtube.com/watch?v=hZj9yfMa130
LESSON 8
MULTIPLICATION AND DIVISION OF NUMBER BASES
MULTIPLICATION is a repeated addition. This principle is always applied while multiplying binary numbers and other number bases. The important thing we must note is that if we are working in base two and other bases, all the figures we use in the working should be less than 2 or the number base under consideration.

https://www.youtube.com/watch?v=k6nO3EGVhfw
DIVISION in base two is very similar to division in base ten. If the two numbers are in the same base, we divide using the long division method. However, if both numbers are not in the same base, we convert to base ten and then to the base required before solving.

https://www.youtube.com/watch?v=JYTHm7HBInQ
ASSIGNMENT
Nelson Functional Mathematics for JSS Book3, Graduated Exercises Page 24-25,Qustions 4, 26-35.
Nelson Functional Mathematical for JSS WorkBook3, Page 2-3,Qustions d and e
Read...
Nelson functional Mathematics for JSS Book3, Page 1-25.
New General Mathematics for JSS3 UBE Edition, Page 14-22.
Nelson functional Mathematics for JSS WorkBook3, Page 1-7.
WEEK 2
TOPIC: USE OF MATHEMATICS IN ICT
CONTENT:
Definition of Computer and ICT
Use of Mathematics in ICT
Using computer to do simple Mathematical calculations.
Translation of word problems into numerical expressions.

LESSON 9
DEFINITION OF COMPUTER AND ICT
Computer is an electronic device that aids computation, storage of information, processing of data, etc.
ICT is an abbreviation for Information and Communication Technology. It is a modern way of processing and distributing data using computer hardware and software, telecommunications, and digital electronics. The computer is configured based on the binary number system only, that is 0 and 1.
USE OF MATHEMATICS IN ICT
The most important aspect of mathematics that aid efficiency of computer is the binary number 0 and 1. These two digits (1 and 0) help the computer to process, store or process and store in:
Hard disk 2. magnetic tape 3. Memory cards 4. Flash drives
Punch card 6. Punch tape 7. Compact disk 8. Diskette e.t.c
https://youtu.be/Z00RA9HJFoc
USING COMPUTER TO DO SIMPLE MATHEMATICAL CALCULATIONS
With the introduction of Information Technology (IT), doing simple Mathematical calculations on computer is now more easier and interesting. The soft wares written on mathematics that make calculations easier are called Mathematics Compact Discs. Examples of mathematics soft wares are Encarta Premium, Encarta Kids, Equation solver, Geo-Gebra, triangle solver, etc. Other ICT gadgets or materials that are useful in the teaching and learning of mathematics are: Mathematics tools, power point, encarta dictionary, calculator, search engines, interactive board, etc.
https://youtu.be/4LRS9uEcivU
EVALUATION:
Define Information Communication Technology.
What is Microsoft Mathematics and what is it made of?
List 10 gadgets that are useful in Mathematics.
Further Studies
Read More...
LESSON 10
TRANSLATION OF WORD PROBLEMS INTO NUMERICAL EXPRESSIONS.
The following terms are commonly used in words expressions.
SUM: The sum of two or more numbers is the result obtained when they are added together.
DIFFERENCE: The difference between two numbers is the result obtained when one of the numbers is subtracted from the other.
POSITIVE DIFFERENCE: This implies larger number minus smaller number.
NEGATIVE DIFFERENCE: This implies smaller number minus larger number
NOTE: When the nature of the difference required is not stated, we consider the positive difference.
PRODUCT: When two or more numbers are multiplied together, the result obtained is known as the product of the numbers.
QUOTIENT: The quotient of two numbers is the result obtained by dividing one number by another.
Examples:
Translate the following word problems into numerical expressions.
From the sum of 78 and 129 subtract 264
Solution:
(78 +129)-264
What must be multiplied by 0.75 to obtain 6?
Solution:
Let the number be x ⟹x(0.75)=6
Add 18 to the negative difference between 56 and 45.
Solution:
(45-56)+18
https://youtu.be/ovT70xTQ000
https://youtu.be/Q08Rhohm5XE
EVALUATION:
Translate the following word problems into numerical expressions.
When a number is trebled and five times the number is subtracted, the result is 3.7
The sum of three consecutive numbers is 108.
Divide the sum of 12 and -4 by the sum of -12 and 4.
If n is doubled and 7 subtracted, the result is 23.
The difference between a certain number and -8 is 15.
ASSIGNMENT
Nelson Functional Mathematical for JSS WorkBook3, Page 18, Questions B(a-d)
READING
Nelson functional Mathematics for JSS Book3, Page 1-25.
New General Mathematics for JSS3 UBE Edition, Page 50-64.
CONTENT:
Definition of Computer and ICT
Use of Mathematics in ICT
Using computer to do simple Mathematical calculations.
Translation of word problems into numerical expressions.

LESSON 9
DEFINITION OF COMPUTER AND ICT
Computer is an electronic device that aids computation, storage of information, processing of data, etc.
ICT is an abbreviation for Information and Communication Technology. It is a modern way of processing and distributing data using computer hardware and software, telecommunications, and digital electronics. The computer is configured based on the binary number system only, that is 0 and 1.
USE OF MATHEMATICS IN ICT
The most important aspect of mathematics that aid efficiency of computer is the binary number 0 and 1. These two digits (1 and 0) help the computer to process, store or process and store in:
Hard disk 2. magnetic tape 3. Memory cards 4. Flash drives
Punch card 6. Punch tape 7. Compact disk 8. Diskette e.t.c
https://youtu.be/Z00RA9HJFoc
USING COMPUTER TO DO SIMPLE MATHEMATICAL CALCULATIONS
With the introduction of Information Technology (IT), doing simple Mathematical calculations on computer is now more easier and interesting. The soft wares written on mathematics that make calculations easier are called Mathematics Compact Discs. Examples of mathematics soft wares are Encarta Premium, Encarta Kids, Equation solver, Geo-Gebra, triangle solver, etc. Other ICT gadgets or materials that are useful in the teaching and learning of mathematics are: Mathematics tools, power point, encarta dictionary, calculator, search engines, interactive board, etc.
https://youtu.be/4LRS9uEcivU
EVALUATION:
Define Information Communication Technology.
What is Microsoft Mathematics and what is it made of?
List 10 gadgets that are useful in Mathematics.
Further Studies
Read More...
LESSON 10
TRANSLATION OF WORD PROBLEMS INTO NUMERICAL EXPRESSIONS.
The following terms are commonly used in words expressions.
SUM: The sum of two or more numbers is the result obtained when they are added together.
DIFFERENCE: The difference between two numbers is the result obtained when one of the numbers is subtracted from the other.
POSITIVE DIFFERENCE: This implies larger number minus smaller number.
NEGATIVE DIFFERENCE: This implies smaller number minus larger number
NOTE: When the nature of the difference required is not stated, we consider the positive difference.
PRODUCT: When two or more numbers are multiplied together, the result obtained is known as the product of the numbers.
QUOTIENT: The quotient of two numbers is the result obtained by dividing one number by another.
Examples:
Translate the following word problems into numerical expressions.
From the sum of 78 and 129 subtract 264
Solution:
(78 +129)-264
What must be multiplied by 0.75 to obtain 6?
Solution:
Let the number be x ⟹x(0.75)=6
Add 18 to the negative difference between 56 and 45.
Solution:
(45-56)+18
https://youtu.be/ovT70xTQ000
https://youtu.be/Q08Rhohm5XE
EVALUATION:
Translate the following word problems into numerical expressions.
When a number is trebled and five times the number is subtracted, the result is 3.7
The sum of three consecutive numbers is 108.
Divide the sum of 12 and -4 by the sum of -12 and 4.
If n is doubled and 7 subtracted, the result is 23.
The difference between a certain number and -8 is 15.
ASSIGNMENT
Nelson Functional Mathematical for JSS WorkBook3, Page 18, Questions B(a-d)
READING
Nelson functional Mathematics for JSS Book3, Page 1-25.
New General Mathematics for JSS3 UBE Edition, Page 50-64.
WEEK 3
TOPIC: WHOLE NUMBERS
CONTENT:
Expressions involving brackets and fractions
Definition and types of proportion
Practical application of proportion
Solving word problems.
LESSON 11
EXPRESSIONS INVOLVING BRACKETS AND FRACTIONS
Here, we combine products with sums and differences. We should note that, when brackets are used in any expression, it indicates multiplication and after the multiplication is completed, the brackets are no longer necessary.
Examples:
Find the product of 16 and the positive difference between 12 and 19.
Solution:
16(19-12)=16×7=112.
Find the sum of the product of 16 and 1/4 and the sum of 1/2 and 3 1/2.
Solution:
(16×1/4)+(1/2+3 1/2)=4+4=8
Find the sum of the product of 2/5 and 3/4 and the product of 1/2 and 2 1/4.
Solution:
(2/5×3/4)+(1/2×2 1/4)=3/10+9/8=(12+45)/40=57/40=1 17/40
Evaluate 1/4 (25-5)
Solution:
1/4 (25-5)=1/4 (20)=20/4=5.
https://youtu.be/rZY3_0JA2SA
EVALUATION:
Divide 42 by the sum of 2 and 4.
Find one –eighth of the sum 18 and the product of 6 and 12.
Find the positive difference between the following pairs of numbers: (a) 6.8 and 12.2 (b). 13 1/2 and 16 2/3.

LESSON 12
PROPORTION
Proportion describes the relationship between two quantities such that change (increase or decrease) will lead to corresponding change (increase or decrease) in the other. There are two types of proportion, direct and indirect proportion.
DIRECT PROPORTION
When one quantity increase lead to corresponding increase in the other or When one quantity increase lead to corresponding increase in the other, then the quantities are said to be in direct proportion. For example, the more fuel added to a burning fire, the more it burn.
INVERSE PROPORTION
If the proportion is such that when one quantity increases, the other decreases proportionally, then the proportion is said to be inverse.
PRACTICAL APPLICATION OF PROPORTION
Examples:
If 20 labourers can clear a school field for 28 days. How many days would it take 10 labourers to clear the field?
Solution:
20 labourers used 28days
1 labourer will use 20×28=560days
10 labours can clear same field in 560/10=56 days.
10 men can build a wall in 12 days. How long will it take 4 men?
Solution:
10 men built the wall in 12 days.
1 man will build it in 120 days
4 men will build it in 120/4=30days.
EVALUATION:
A nurse counted 30 heart beats in 25 seconds. How many times will the heart beat in 1 minutes.
8 men plough a farmland in 15 days. How many days will it take 5 men working at the same rate?
https://youtu.be/USmit5zUGas
SOLVING WORD PROBLEMS.
Examples:
Find one-quuarter of the positive difference between 15 and 55.
Solution:
1/4 (55-15)=1/4 (40)=10.
Subtract 15 from the product of 5 and 15, then divide the result by 3.
Solution:
((5×15)-15)/3
=60/3
=20.
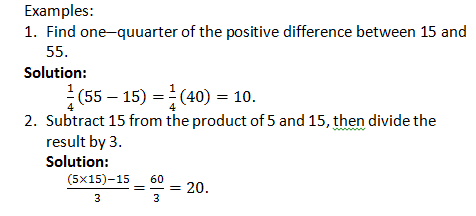
EVALUATION:
Nelson functional Mathematics for JSS Book3, Page 39, Questions 4,6 and 10. Page 32, Questions 3 and 5.
ASSIGNMENT
Nelson Functional Mathematical for JSS WorkBook3, Page 8, Questions B to C. Page 12, Questions a & b
READING
Nelson functional Mathematics for JSS Book3, Page 26-35, 38-40.
LESSON 13
TOPIC: COMPOUND INTEREST
CONTENTS:
Profit and Loss (revision)
simple interest (revision)
Compound interest
Use of compound interest in daily life i.e.
Depreciation
Inflation
PROFIT AND LOSS (REVISION)
When any transaction is done, we either make profit or a loss. When an article is sold at a price greater than the price it was bought, then a profit is made. On the other hand, if an article is sold at a price less than the cost, we have made a loss.
Hence,
Profit = selling price – cost price
Loss = Cost price – selling price
In commercial transactions, profit and loss are usually expressed as a percentage of the cost price.
That is,
profit percent=profit/(cost price)×100%
loss percent=loss/(cost price)×100%
https://youtu.be/R6N2XOGJ8UY
Examples:
A trader bought a book for N75 and sold it for N86. What is the profit percent?
Solution
Cost price = N75
Selling price = N86
Profit = selling price – cost price
= N86- N75 = N11
profit percent=profit/(cost price)×100%
= 11/75×100%
= 14.67%
An article which cost N300 was sold for N225, what is the loss percent?
Solution
Cost price = N300
Selling price = N225
Loss = Cost price – selling price
loss percent=loss/(cost price)×100%
=75/300×100%
= 25%

EVALUATION:
Adamu bought a pair of shoes for N2,000. Find his percentage loss?
Find the cost price of each of these selling prices
N540 at a profit of 25%
N2,500 at a loss of 15%
CONTENT:
Expressions involving brackets and fractions
Definition and types of proportion
Practical application of proportion
Solving word problems.
LESSON 11
EXPRESSIONS INVOLVING BRACKETS AND FRACTIONS
Here, we combine products with sums and differences. We should note that, when brackets are used in any expression, it indicates multiplication and after the multiplication is completed, the brackets are no longer necessary.
Examples:
Find the product of 16 and the positive difference between 12 and 19.
Solution:
16(19-12)=16×7=112.
Find the sum of the product of 16 and 1/4 and the sum of 1/2 and 3 1/2.
Solution:
(16×1/4)+(1/2+3 1/2)=4+4=8
Find the sum of the product of 2/5 and 3/4 and the product of 1/2 and 2 1/4.
Solution:
(2/5×3/4)+(1/2×2 1/4)=3/10+9/8=(12+45)/40=57/40=1 17/40
Evaluate 1/4 (25-5)
Solution:
1/4 (25-5)=1/4 (20)=20/4=5.
https://youtu.be/rZY3_0JA2SA
EVALUATION:
Divide 42 by the sum of 2 and 4.
Find one –eighth of the sum 18 and the product of 6 and 12.
Find the positive difference between the following pairs of numbers: (a) 6.8 and 12.2 (b). 13 1/2 and 16 2/3.

LESSON 12
PROPORTION
Proportion describes the relationship between two quantities such that change (increase or decrease) will lead to corresponding change (increase or decrease) in the other. There are two types of proportion, direct and indirect proportion.
DIRECT PROPORTION
When one quantity increase lead to corresponding increase in the other or When one quantity increase lead to corresponding increase in the other, then the quantities are said to be in direct proportion. For example, the more fuel added to a burning fire, the more it burn.
INVERSE PROPORTION
If the proportion is such that when one quantity increases, the other decreases proportionally, then the proportion is said to be inverse.
PRACTICAL APPLICATION OF PROPORTION
Examples:
If 20 labourers can clear a school field for 28 days. How many days would it take 10 labourers to clear the field?
Solution:
20 labourers used 28days
1 labourer will use 20×28=560days
10 labours can clear same field in 560/10=56 days.
10 men can build a wall in 12 days. How long will it take 4 men?
Solution:
10 men built the wall in 12 days.
1 man will build it in 120 days
4 men will build it in 120/4=30days.
EVALUATION:
A nurse counted 30 heart beats in 25 seconds. How many times will the heart beat in 1 minutes.
8 men plough a farmland in 15 days. How many days will it take 5 men working at the same rate?
https://youtu.be/USmit5zUGas
SOLVING WORD PROBLEMS.
Examples:
Find one-quuarter of the positive difference between 15 and 55.
Solution:
1/4 (55-15)=1/4 (40)=10.
Subtract 15 from the product of 5 and 15, then divide the result by 3.
Solution:
((5×15)-15)/3
=60/3
=20.
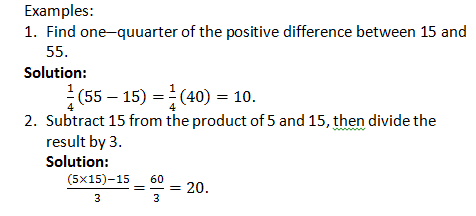
EVALUATION:
Nelson functional Mathematics for JSS Book3, Page 39, Questions 4,6 and 10. Page 32, Questions 3 and 5.
ASSIGNMENT
Nelson Functional Mathematical for JSS WorkBook3, Page 8, Questions B to C. Page 12, Questions a & b
READING
Nelson functional Mathematics for JSS Book3, Page 26-35, 38-40.
LESSON 13
TOPIC: COMPOUND INTEREST
CONTENTS:
Profit and Loss (revision)
simple interest (revision)
Compound interest
Use of compound interest in daily life i.e.
Depreciation
Inflation
PROFIT AND LOSS (REVISION)
When any transaction is done, we either make profit or a loss. When an article is sold at a price greater than the price it was bought, then a profit is made. On the other hand, if an article is sold at a price less than the cost, we have made a loss.
Hence,
Profit = selling price – cost price
Loss = Cost price – selling price
In commercial transactions, profit and loss are usually expressed as a percentage of the cost price.
That is,
profit percent=profit/(cost price)×100%
loss percent=loss/(cost price)×100%
https://youtu.be/R6N2XOGJ8UY
Examples:
A trader bought a book for N75 and sold it for N86. What is the profit percent?
Solution
Cost price = N75
Selling price = N86
Profit = selling price – cost price
= N86- N75 = N11
profit percent=profit/(cost price)×100%
= 11/75×100%
= 14.67%
An article which cost N300 was sold for N225, what is the loss percent?
Solution
Cost price = N300
Selling price = N225
Loss = Cost price – selling price
loss percent=loss/(cost price)×100%
=75/300×100%
= 25%

EVALUATION:
Adamu bought a pair of shoes for N2,000. Find his percentage loss?
Find the cost price of each of these selling prices
N540 at a profit of 25%
N2,500 at a loss of 15%
WEEK 4
LESSON 14
SIMPLE INTEREST (REVISION)
Interest is a payment given for saving money. It can also be the price paid for borrowing money. When interest is calculated on the basic sum of money saved (or borrowed) it is called Simple Interest. Simple interest (I) is calculated using the formula
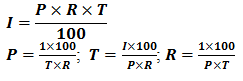
The initial amount is called the Principal (P) (the sum of money saved or borrowed). Rate(R) is the annual rate of interest (given as a percentage).The length of the period in which the principal is used is called the Time (T). The principal plus interest is called the Amount.
Examples:
Find the simple interest on N500 for 4 years at the rate of 5%. What is the amount?
Solution:
Principal = N500
Time = 4 years
Rate = 5%
I=(P×R×T)/100
=(500×5×4)/100 = N100
Amount = Principal + Simple interest
= N500 + N100
= N600
Calculate the interest rate percent per annum for a loan of N5,862 for 3 years and a repayment of N7,895.
Solution:
Amount = N7,895
Principal = N5,862
Time = 3 years
Interest = ?
Rate = ?
But we know that,
Amount = Principal + Interest
Interest = Amount – Principal
= N7,895 - N5,862 = N2,033
I=(P×R×T)/100
R=(1×100)/(P×T)
=(2,033×100)/(5,862×3)=(203,300)/(17,586)=11.56%

EVALUATION:
Find the simple interest on N800 for 3 years at the rate of 60%.
Calculate the simple interest on N8,000 for 2 years at 4% per annum.
LESSON 15
COMPOUND INTEREST:
In compound interest, interest is calculated and added to the principal at the end of each interval, thus the principal increases and so the interest becomes larger for each interval. Most saving schemes give compound interest not simple. The total value at the end of the investment is the compound amount.
Thus,
Compound amount = compound interest + principal
Example:
Calculate the compound interest on N6,000 for 4 years at 10% per annum. What is the compound amount?
Solution
First year:
Principal = N6,000
interest=(6,000×10×1)/100
= N600
Amount at the end of the 1st year = (N6,000+ N600)
= N6,600
Second year:
Principal = N6,600
interest=(6,600×10×1)/100
= N660
Amount at the end of the 2nd year = (N6,600+ N660)
= N7,260
Third year:
Principal = N7,260
interest=(7,260×10×1)/100
= N726
Amount at the end of the 3rd year = (N7,260+N726)
= N7,986
Fourth year:
Principal = N7,986
interest=(7,986×10×1)/100 = N798.60
Amount at the end of the 4th year = (N7,986+ N798.60) = N8,784.60
Compound amount = N8,784.60
Compound interest = N8,784.60 - N6,000 = N2,784.00

EVALUATION:
Find the compound amount and interest on N4,000 at 15% for 2 years.
LESSON 16
DEPRECIATION
Most of items such as radios, cars clothing, houses, and electrical goods lose value as time passes. This loss in value is called depreciation. Depreciation is usually given as a percentage of the item’s value at the beginning of the year
Example:
A car costing N680,000 depreciates by 25% in its first year and 20% in its second year. Find its value after 2 years.
Solution
1st year: value of car is N680,000
25% depreciation =680,000-(25⁄100×680,000)
= N680,000 - N170,000
= N510,000
2nd year: value of car is N510,000
20% depreciation =510,000-(□(20/100×510,000))
= N510,000 – N102,000
=N408,000
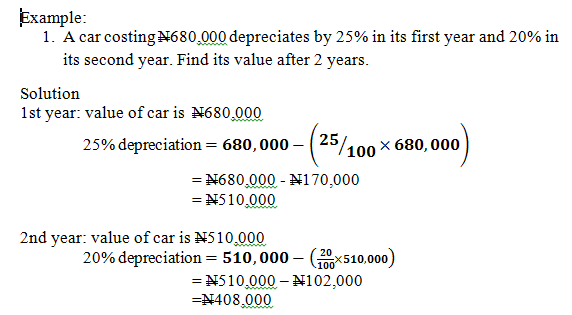
INFLATION
Due to rising prices, money loses its value as time passes. Lose in value of money is called Inflation. Inflation is usually given as the percentage increase in the cost of buying things from year to the next.
Example:
How long will it take for prices to double if the rate of inflation is 20% per annum?
Solution:
Start with an initial cost of 100 units.
Initial cost = 100
Rise = 20% of 100
=20/100×100=20
After 1 year, cost = 100 + 20 = 120
Rise =20/100×120=24
After 2 years, cost = 120 + 24 =144
Rise =20/100×144=28.8
After 3 years, cost =144+28.8 =172.8
Rise =20/100×172.8=34.56
After 4 years, cost = 172.8 + 34.56
= 207. 36
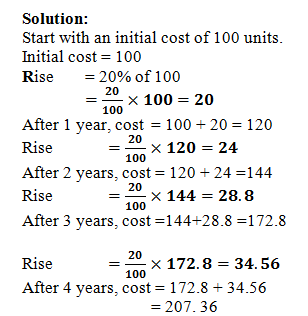
The cost after 4 years is a little more than double of initial cost. Hence prices will double in just under 4 years.
ASSIGNMENT:
Nelson Functional Mathematics for Junior Secondary Schools Workbook 3. Pg 21 C. Compound Interest from (b)-(e)
READING:
Nelson Functional Mathematics for Junior Secondary Schools Book 3. Pg 65-71
SIMPLE INTEREST (REVISION)
Interest is a payment given for saving money. It can also be the price paid for borrowing money. When interest is calculated on the basic sum of money saved (or borrowed) it is called Simple Interest. Simple interest (I) is calculated using the formula
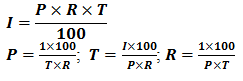
The initial amount is called the Principal (P) (the sum of money saved or borrowed). Rate(R) is the annual rate of interest (given as a percentage).The length of the period in which the principal is used is called the Time (T). The principal plus interest is called the Amount.
Examples:
Find the simple interest on N500 for 4 years at the rate of 5%. What is the amount?
Solution:
Principal = N500
Time = 4 years
Rate = 5%
I=(P×R×T)/100
=(500×5×4)/100 = N100
Amount = Principal + Simple interest
= N500 + N100
= N600
Calculate the interest rate percent per annum for a loan of N5,862 for 3 years and a repayment of N7,895.
Solution:
Amount = N7,895
Principal = N5,862
Time = 3 years
Interest = ?
Rate = ?
But we know that,
Amount = Principal + Interest
Interest = Amount – Principal
= N7,895 - N5,862 = N2,033
I=(P×R×T)/100
R=(1×100)/(P×T)
=(2,033×100)/(5,862×3)=(203,300)/(17,586)=11.56%

EVALUATION:
Find the simple interest on N800 for 3 years at the rate of 60%.
Calculate the simple interest on N8,000 for 2 years at 4% per annum.
LESSON 15
COMPOUND INTEREST:
In compound interest, interest is calculated and added to the principal at the end of each interval, thus the principal increases and so the interest becomes larger for each interval. Most saving schemes give compound interest not simple. The total value at the end of the investment is the compound amount.
Thus,
Compound amount = compound interest + principal
Example:
Calculate the compound interest on N6,000 for 4 years at 10% per annum. What is the compound amount?
Solution
First year:
Principal = N6,000
interest=(6,000×10×1)/100
= N600
Amount at the end of the 1st year = (N6,000+ N600)
= N6,600
Second year:
Principal = N6,600
interest=(6,600×10×1)/100
= N660
Amount at the end of the 2nd year = (N6,600+ N660)
= N7,260
Third year:
Principal = N7,260
interest=(7,260×10×1)/100
= N726
Amount at the end of the 3rd year = (N7,260+N726)
= N7,986
Fourth year:
Principal = N7,986
interest=(7,986×10×1)/100 = N798.60
Amount at the end of the 4th year = (N7,986+ N798.60) = N8,784.60
Compound amount = N8,784.60
Compound interest = N8,784.60 - N6,000 = N2,784.00

EVALUATION:
Find the compound amount and interest on N4,000 at 15% for 2 years.
LESSON 16
DEPRECIATION
Most of items such as radios, cars clothing, houses, and electrical goods lose value as time passes. This loss in value is called depreciation. Depreciation is usually given as a percentage of the item’s value at the beginning of the year
Example:
A car costing N680,000 depreciates by 25% in its first year and 20% in its second year. Find its value after 2 years.
Solution
1st year: value of car is N680,000
25% depreciation =680,000-(25⁄100×680,000)
= N680,000 - N170,000
= N510,000
2nd year: value of car is N510,000
20% depreciation =510,000-(□(20/100×510,000))
= N510,000 – N102,000
=N408,000
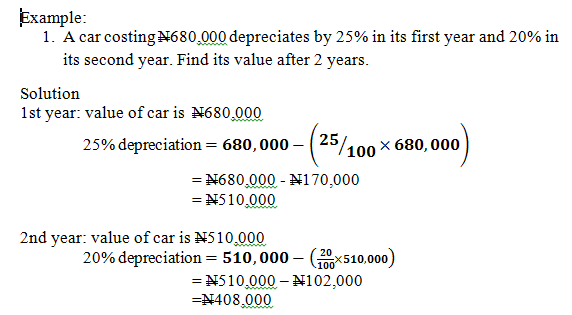
INFLATION
Due to rising prices, money loses its value as time passes. Lose in value of money is called Inflation. Inflation is usually given as the percentage increase in the cost of buying things from year to the next.
Example:
How long will it take for prices to double if the rate of inflation is 20% per annum?
Solution:
Start with an initial cost of 100 units.
Initial cost = 100
Rise = 20% of 100
=20/100×100=20
After 1 year, cost = 100 + 20 = 120
Rise =20/100×120=24
After 2 years, cost = 120 + 24 =144
Rise =20/100×144=28.8
After 3 years, cost =144+28.8 =172.8
Rise =20/100×172.8=34.56
After 4 years, cost = 172.8 + 34.56
= 207. 36
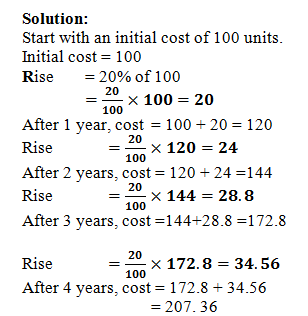
The cost after 4 years is a little more than double of initial cost. Hence prices will double in just under 4 years.
ASSIGNMENT:
Nelson Functional Mathematics for Junior Secondary Schools Workbook 3. Pg 21 C. Compound Interest from (b)-(e)
READING:
Nelson Functional Mathematics for Junior Secondary Schools Book 3. Pg 65-71
WEEK 5
LESSON 17
TOPIC: CONVERSION OF BASE 10 NUMERALS TO BINARY NUMBERS
CONTENTS:
Binary number (Converting numbers between 1-10 to base 2)
Quantitative reasoning (using conversion of numerals from base 10 to base 2)
BINARY NUMBER (CONVERTING NUMBERS BETWEEN 1-10 TO BASE 2)
The binary or base two system is based on the number two. The binary system is second in importance to our usual base ten systems. Its importance is due to the fact that it is used by computers for numerical calculations. Binary numbers are made up of two digits, 1 and 0. A computer contains a large number of switches. Each switch is either ‘on’ or ‘off’. An ‘on’ switch represents 1; an ‘off’ switch represents 0.
Note: In converting any number in base ten to base two, divide by two and retrieve the remainder from the rear.
https://youtu.be/jdfrwxUkXOk
Example
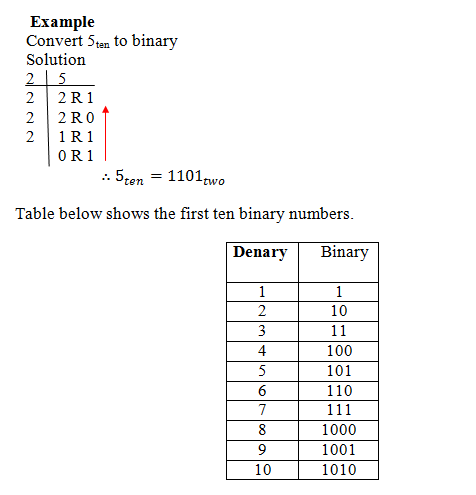
Convert 5ten to binary
Solution
2 5
2 2 R 1
2 2 R 0
2 1 R 1
0 R 1
∴5_ten=〖1101〗_two
Table below shows the first ten binary numbers.
Denary
Binary
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
EVALUATION
Convert the following denary numbers to binary
27
35
LESSON 18
QUANTITATIVE REASONING
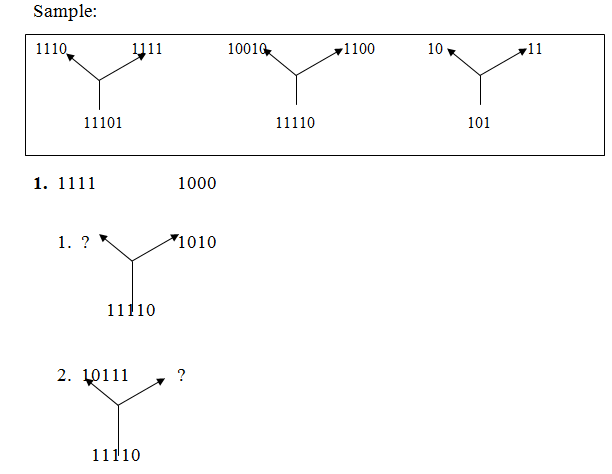
https://youtu.be/NEJXqFw999o
EVALUATION:
Use the sample below to evaluate questions 1-3
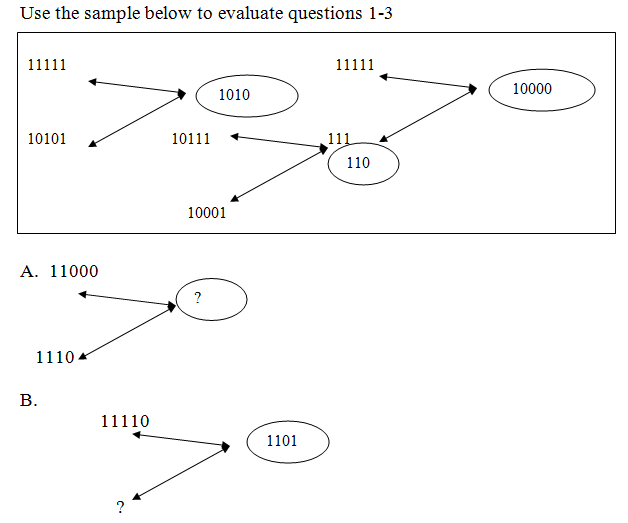
ASSIGNMENT:
Convert denary numbers between 11-20 to binary
Use the sample below to answer questions a – c leaving your answer in binary base.
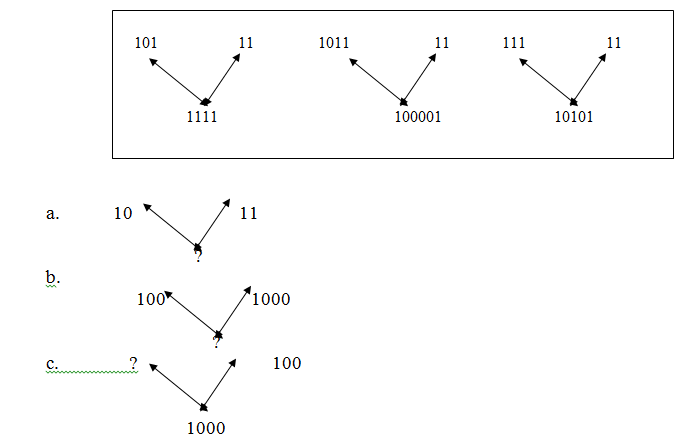
READING:
Nelson Functional Mathematics for JSS Book 3, Pg 10-12.
TOPIC: CONVERSION OF BASE 10 NUMERALS TO BINARY NUMBERS
CONTENTS:
Binary number (Converting numbers between 1-10 to base 2)
Quantitative reasoning (using conversion of numerals from base 10 to base 2)
BINARY NUMBER (CONVERTING NUMBERS BETWEEN 1-10 TO BASE 2)
The binary or base two system is based on the number two. The binary system is second in importance to our usual base ten systems. Its importance is due to the fact that it is used by computers for numerical calculations. Binary numbers are made up of two digits, 1 and 0. A computer contains a large number of switches. Each switch is either ‘on’ or ‘off’. An ‘on’ switch represents 1; an ‘off’ switch represents 0.
Note: In converting any number in base ten to base two, divide by two and retrieve the remainder from the rear.
https://youtu.be/jdfrwxUkXOk
Example
Convert 5ten to binary
Solution
2 5
2 2 R 1
2 2 R 0
2 1 R 1
0 R 1
∴5_ten=〖1101〗_two
Table below shows the first ten binary numbers.
Denary
Binary
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010

EVALUATION
Convert the following denary numbers to binary
27
35
LESSON 18
QUANTITATIVE REASONING

https://youtu.be/NEJXqFw999o
EVALUATION:
Use the sample below to evaluate questions 1-3

ASSIGNMENT:
Convert denary numbers between 11-20 to binary
Use the sample below to answer questions a – c leaving your answer in binary base.

READING:
Nelson Functional Mathematics for JSS Book 3, Pg 10-12.
WEEK 6
LESSON 19
TOPIC: COMPUTER APPLICATIONS
CONTENTS:
Use of punched card to store information
Writing familiar words in coded form
USE OF PUNCHED CARD TO STORE INFORMATION
Cards are used to store and keep information about people or things. The binary number system is usually used to store information on the cards. The process involves a hole punched out (0) or a slot cut out (1). Any information that can be classified as a two-way coding system can be stored on such cards.

Figure above shows a card for a student, Ita Akpan. In a survey, it is found that Isa plays volley ball and hockey but not football or tennis. If 1 represents a game played and 0 a game not played, each possible combination of games can be represented by a binary number. What is the number for the games played by Isa?
https://youtu.be/oPKmegMkJrI
EVALUATION:
1. Why has the corner been cut off the card above?
2. Sketch a card for a student who plays football and hockey only.
3. Which games are played by students whose cards represent the numbers
i) 1 011,
ii) 0 010
iii) 1 101,
iv) 1 001?
LESSON 20
Writing Familiar Words in Coded Form
Study the table below:
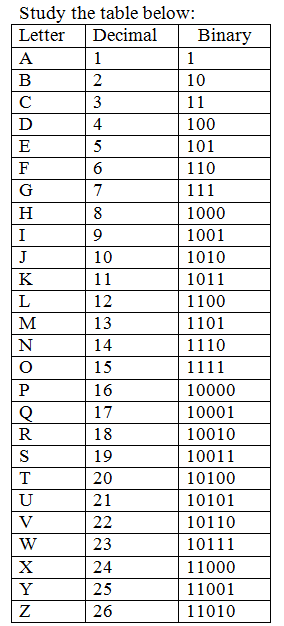
Example 2:
Write John Ado Sule using 0 – 1 coding format.
Solution
Method 1:
(1010) (1111) (1000) (1110)
(1) (100) (1111)
(10011) (10101) (1100) (101)
Method 2: A letter per line code
1010 = J
1111 =O
1000 =H
1110 =N
1 =A
100 =D
1111 =O
10011 = S
10101 = U
1100 =L
101 =E
https://youtu.be/WhWEbcbX5Ug
https://youtu.be/FCFWu4NlUJQ
EVALUATION:
Write your name using 0 – 1 coding format.
ASSIGNMENT:
Nelson Functional Mathematics for Junior Secondary Schools Book 3. Pg 63 Graduated Exercises 3,4,7,13,21
READING:
Nelson Functional Mathematics for Junior Secondary Schools Book 3. Pg 50-64
TOPIC: COMPUTER APPLICATIONS
CONTENTS:
Use of punched card to store information
Writing familiar words in coded form
USE OF PUNCHED CARD TO STORE INFORMATION
Cards are used to store and keep information about people or things. The binary number system is usually used to store information on the cards. The process involves a hole punched out (0) or a slot cut out (1). Any information that can be classified as a two-way coding system can be stored on such cards.

Figure above shows a card for a student, Ita Akpan. In a survey, it is found that Isa plays volley ball and hockey but not football or tennis. If 1 represents a game played and 0 a game not played, each possible combination of games can be represented by a binary number. What is the number for the games played by Isa?
https://youtu.be/oPKmegMkJrI
EVALUATION:
1. Why has the corner been cut off the card above?
2. Sketch a card for a student who plays football and hockey only.
3. Which games are played by students whose cards represent the numbers
i) 1 011,
ii) 0 010
iii) 1 101,
iv) 1 001?
LESSON 20
Writing Familiar Words in Coded Form
Study the table below:

Example 2:
Write John Ado Sule using 0 – 1 coding format.
Solution
Method 1:
(1010) (1111) (1000) (1110)
(1) (100) (1111)
(10011) (10101) (1100) (101)
Method 2: A letter per line code
1010 = J
1111 =O
1000 =H
1110 =N
1 =A
100 =D
1111 =O
10011 = S
10101 = U
1100 =L
101 =E
https://youtu.be/WhWEbcbX5Ug
https://youtu.be/FCFWu4NlUJQ
EVALUATION:
Write your name using 0 – 1 coding format.
ASSIGNMENT:
Nelson Functional Mathematics for Junior Secondary Schools Book 3. Pg 63 Graduated Exercises 3,4,7,13,21
READING:
Nelson Functional Mathematics for Junior Secondary Schools Book 3. Pg 50-64
WEEK 7
TOPIC: FACTORIZATION
CONTENTS:
Removing brackets (revision)
Factorization by taking Common factors
Factorization by grouping
Expanding algebraic expressions
Factorization of quadratic expressions
Perfect squares
Difference of two squares
Word Problems Involving Factorization
LESSON 21
REMOVING BRACKETS (REVISION)
Example 1
Remove brackets from
3(2u - v)
(3a+8b)5a
-2n(7y – 4z)
Solutions
3(2u - v) = 3 x 2u + 3 x v
= 6u + 3v
(3a + 8b)5a =3a x 5a + 8b x 5a
=15a2 + 40ab
-2n(7y – 4z) =(-2n) x 7y – (-2n) x 4z
= -14ny + 8ny
https://youtu.be/bOTOcZXvUV8
FACTORIZATION BY TAKING COMMON FACTORS
To factorize an expression is to write it as a product of its factors
Example
Factorize the following:
9a – 3z
5x2 + 15x
Factorize 2x(5a+2)-3y(5a+2)
Solution:
The HCF of 9a and 3z is 3
9a-3z=3(□(9a/3-□(3z/3)) )
= 3(3a – z)
The HCF of 5x2 and 15x is 5x
5x2+ 15x=5x(□((5x2)/5x)+□(15x/5x))
= 5x(x+3)
Factorize 2x(5a+2)-3y(5a+2)
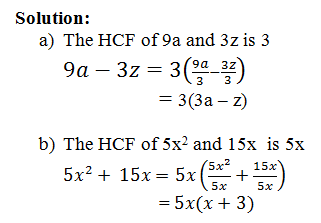
In the given expression,
2x(5a+2)= 2x times (5a+2)
3y(5a+2)= 3y times (5a+2)
Hence the products 2x(5a+2)and 3y(5a+2)
have the factor (5a+2) in common. Thus,
2x(5a+2)-3y(5a+2)=(5a+2)(2x-3y)
EVALUATION:
Remove brackets from the following:
i) 8(2a-3b) ii) -3(a-b) iii) (r+h)2πr
Factorize the following:
i) 5a +5z ii) 33bd-3de
https://youtu.be/6PWXdE2hRO4
LESSON 22
FACTORIZATION BY GROUPING
Example
Factorize the following:
cx+cy+2dx+2dy.
3a-6b+ax-2bx.
Solution:
cx+cy+2dx+2dy.
The terms cx and cy have c in common.
The terms 2dx and 2dy have 2d in common.
Grouping in pairs in this way,
cx+cy+2dx+2dy=(cx+cy)+(2dx+2dy)
= c(x+y)+2d(x+y)
The two products now have (x+y) in common.
∴c(x+y)+2d(x+y) = (x+y)+(c+2d)
https://youtu.be/9hSZEzBmG6M
EXPANDING ALGEBRAIC EXPRESSIONS
Example
Find the product of (x+2) and (x-5)
(The expression (x+2) (x-5) means (x+2) × (x-5).
The product of (x+2) and (x-5) is found by multiplying each term in the first bracket by each term in the second bracket.)
(x+2)(x-5)=x(x+2)-5(x+2)
=x2+ 2x-5x-10
=x2-3x-10
Expand (3a +2)2.
Solution
(3a+2)2=(3a+2)(3a+2)
=3a(3a+2)+2(3a+2)
=9a2+6a+6a+4
=9a2+12a+4
EVALUATION:
Expand the following:
i. (〖a+b)〗2
ii. (〖x-y)〗2
iii. (〖1+2f)〗2
https://youtu.be/iXRsIswFPYU
LESSON 23
FACTORIZATION OF QUADRATIC EXPRESSIONS
A quadratic expression is one in which 2 is the highest power of the unknown(s) in the expression. For example, x2-4x-12,16-a2,〖3x〗2+17xy+〖10y〗2 are all quadratic expressions.
To factorize a quadratic expression is to express it as a product of its factors.
NOTE: A quadratic expression may not have other factors other than itself and 1. For example, x2+2x-6. This type of quadratic expression cannot be factorized.
Example
Factorize the following quadratic expressions:
x2+7x+10
d2+11x+18
Solution
x2+7x+10
1st step: x2+7x+10=( x )( x )
since the first term in the given expression is x2.
2nd step: Find two numbers such that their product is +10 and their sum is +7.
Number pair which has a product of +10 sums of factors
+10 and +1 +11
+5 and +2 +7
-10 and -1 -11
-5 and -2 -7
Of these, only ii) gives the required result; Thus,
x2+7x+10=( x+5)( x +2)
Note 1. The answer can be checked by expanding the brackets.
2. The order of the brackets is not important.
( x+2)( x +5)=( x+5)( x +2)
d2+11x+18
1st step: d2+11x+18=( d )( d )
since the first term in the given expression is d2.
2nd step: Find two numbers such that their product is +18 and their sum is +11. Since the 18 is positive, consider the 11 is positive, consider positive factors only
Factors of +10 sums of factors
+18 and +1 +19
+9 and +2 +11
+6 and +3 +9
Of these, only ii) gives the required result; Thus,
d2+11x+18=( d + 2)( d+9)
EVALUATION:
Factorize the following:
i) x2-4x+3 ii) p2-11p+24
https://youtu.be/yfiMho1_t4k
LESSON 24
DIFFERENCE OF TWO SQUARES
The difference of the squares of two quantities is equal to the product of their sum and their difference.
(a+b)(a-b)=a2+ab-ab-b2=a2-b2
Hence a2-b2=(a-b)(a+b)
Examples:
Factorize the following:
y2 – 4
36 – 9a2
5m2 – 45
πR2-πr2
Solution
y2 – 4 = (y)2 – (2)2
= (y-2) (y+2)
36 – 9a2 = (6)2 – (3a)2
= (6-3a) (6+3a)
5m2 – 45 = 5(m2 – 9)
= 5(m2 – 32)
= 5(m+3)(m-3)
πR2-πr2 = π〖(R〗2-r2)
= π(R-r)(R+r)
EVALUATION
Factorize the following:
i) x2-1 ii) 〖4g〗2-4 iii) 100 – w2
https://youtu.be/H21qt027H48
LESSON 25
WORD PROBLEMS INVOLVING FACTORIZATION
Figure below shows a circular metal washer. If the diameters of the washer and its hole are 3cm and 1cm respectively, find the area of the washer. Use the value 3.14 for π.

SOLUTION
Let the outer and inner radii of the washer be R and r respectively.
Area of washer = πR2-πr2
= π〖(R〗2-r2)
= π(R-r)(R+r)
But,
Radius (R)=3/2=1.5cm,
radius(r)= 0.5cm
∴ Area of washer = π(1.5-0.5)(1.5+0.5)〖cm〗2
= π×1×2 = 2 ×π〖cm〗2
= 2 ×3.14 = 6.28〖cm〗2
ASSIGNMENT:
Expand and find the coefficient of d in the expansion of the following expressions?
(d + 2) (d + 7) ii) (d – 8)(d + 3)
Factorize the following:
s2 + 10s +16 ii) n2 -7n + 10 iii) 36a2 -49b2 iv)100x2-1
x2 y2-z2
New General Mathematics for JSS Book3 pg29-34.
Further Studies
https://youtu.be/DjuNujTgL0E
https://youtu.be/TZWqkjraLWQ
https://youtu.be/lS9S1iEjlPI
CONTENTS:
Removing brackets (revision)
Factorization by taking Common factors
Factorization by grouping
Expanding algebraic expressions
Factorization of quadratic expressions
Perfect squares
Difference of two squares
Word Problems Involving Factorization
LESSON 21
REMOVING BRACKETS (REVISION)
Example 1
Remove brackets from
3(2u - v)
(3a+8b)5a
-2n(7y – 4z)
Solutions
3(2u - v) = 3 x 2u + 3 x v
= 6u + 3v
(3a + 8b)5a =3a x 5a + 8b x 5a
=15a2 + 40ab
-2n(7y – 4z) =(-2n) x 7y – (-2n) x 4z
= -14ny + 8ny
https://youtu.be/bOTOcZXvUV8
FACTORIZATION BY TAKING COMMON FACTORS
To factorize an expression is to write it as a product of its factors
Example
Factorize the following:
9a – 3z
5x2 + 15x
Factorize 2x(5a+2)-3y(5a+2)
Solution:
The HCF of 9a and 3z is 3
9a-3z=3(□(9a/3-□(3z/3)) )
= 3(3a – z)
The HCF of 5x2 and 15x is 5x
5x2+ 15x=5x(□((5x2)/5x)+□(15x/5x))
= 5x(x+3)
Factorize 2x(5a+2)-3y(5a+2)
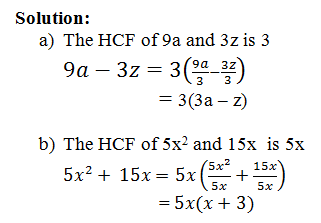
In the given expression,
2x(5a+2)= 2x times (5a+2)
3y(5a+2)= 3y times (5a+2)
Hence the products 2x(5a+2)and 3y(5a+2)
have the factor (5a+2) in common. Thus,
2x(5a+2)-3y(5a+2)=(5a+2)(2x-3y)
EVALUATION:
Remove brackets from the following:
i) 8(2a-3b) ii) -3(a-b) iii) (r+h)2πr
Factorize the following:
i) 5a +5z ii) 33bd-3de
https://youtu.be/6PWXdE2hRO4
LESSON 22
FACTORIZATION BY GROUPING
Example
Factorize the following:
cx+cy+2dx+2dy.
3a-6b+ax-2bx.
Solution:
cx+cy+2dx+2dy.
The terms cx and cy have c in common.
The terms 2dx and 2dy have 2d in common.
Grouping in pairs in this way,
cx+cy+2dx+2dy=(cx+cy)+(2dx+2dy)
= c(x+y)+2d(x+y)
The two products now have (x+y) in common.
∴c(x+y)+2d(x+y) = (x+y)+(c+2d)
https://youtu.be/9hSZEzBmG6M
EXPANDING ALGEBRAIC EXPRESSIONS
Example
Find the product of (x+2) and (x-5)
(The expression (x+2) (x-5) means (x+2) × (x-5).
The product of (x+2) and (x-5) is found by multiplying each term in the first bracket by each term in the second bracket.)
(x+2)(x-5)=x(x+2)-5(x+2)
=x2+ 2x-5x-10
=x2-3x-10
Expand (3a +2)2.
Solution
(3a+2)2=(3a+2)(3a+2)
=3a(3a+2)+2(3a+2)
=9a2+6a+6a+4
=9a2+12a+4
EVALUATION:
Expand the following:
i. (〖a+b)〗2
ii. (〖x-y)〗2
iii. (〖1+2f)〗2
https://youtu.be/iXRsIswFPYU
LESSON 23
FACTORIZATION OF QUADRATIC EXPRESSIONS
A quadratic expression is one in which 2 is the highest power of the unknown(s) in the expression. For example, x2-4x-12,16-a2,〖3x〗2+17xy+〖10y〗2 are all quadratic expressions.
To factorize a quadratic expression is to express it as a product of its factors.
NOTE: A quadratic expression may not have other factors other than itself and 1. For example, x2+2x-6. This type of quadratic expression cannot be factorized.
Example
Factorize the following quadratic expressions:
x2+7x+10
d2+11x+18
Solution
x2+7x+10
1st step: x2+7x+10=( x )( x )
since the first term in the given expression is x2.
2nd step: Find two numbers such that their product is +10 and their sum is +7.
Number pair which has a product of +10 sums of factors
+10 and +1 +11
+5 and +2 +7
-10 and -1 -11
-5 and -2 -7
Of these, only ii) gives the required result; Thus,
x2+7x+10=( x+5)( x +2)
Note 1. The answer can be checked by expanding the brackets.
2. The order of the brackets is not important.
( x+2)( x +5)=( x+5)( x +2)
d2+11x+18
1st step: d2+11x+18=( d )( d )
since the first term in the given expression is d2.
2nd step: Find two numbers such that their product is +18 and their sum is +11. Since the 18 is positive, consider the 11 is positive, consider positive factors only
Factors of +10 sums of factors
+18 and +1 +19
+9 and +2 +11
+6 and +3 +9
Of these, only ii) gives the required result; Thus,
d2+11x+18=( d + 2)( d+9)
EVALUATION:
Factorize the following:
i) x2-4x+3 ii) p2-11p+24
https://youtu.be/yfiMho1_t4k
LESSON 24
DIFFERENCE OF TWO SQUARES
The difference of the squares of two quantities is equal to the product of their sum and their difference.
(a+b)(a-b)=a2+ab-ab-b2=a2-b2
Hence a2-b2=(a-b)(a+b)
Examples:
Factorize the following:
y2 – 4
36 – 9a2
5m2 – 45
πR2-πr2
Solution
y2 – 4 = (y)2 – (2)2
= (y-2) (y+2)
36 – 9a2 = (6)2 – (3a)2
= (6-3a) (6+3a)
5m2 – 45 = 5(m2 – 9)
= 5(m2 – 32)
= 5(m+3)(m-3)
πR2-πr2 = π〖(R〗2-r2)
= π(R-r)(R+r)
EVALUATION
Factorize the following:
i) x2-1 ii) 〖4g〗2-4 iii) 100 – w2
https://youtu.be/H21qt027H48
LESSON 25
WORD PROBLEMS INVOLVING FACTORIZATION
Figure below shows a circular metal washer. If the diameters of the washer and its hole are 3cm and 1cm respectively, find the area of the washer. Use the value 3.14 for π.

SOLUTION
Let the outer and inner radii of the washer be R and r respectively.
Area of washer = πR2-πr2
= π〖(R〗2-r2)
= π(R-r)(R+r)
But,
Radius (R)=3/2=1.5cm,
radius(r)= 0.5cm
∴ Area of washer = π(1.5-0.5)(1.5+0.5)〖cm〗2
= π×1×2 = 2 ×π〖cm〗2
= 2 ×3.14 = 6.28〖cm〗2
ASSIGNMENT:
Expand and find the coefficient of d in the expansion of the following expressions?
(d + 2) (d + 7) ii) (d – 8)(d + 3)
Factorize the following:
s2 + 10s +16 ii) n2 -7n + 10 iii) 36a2 -49b2 iv)100x2-1
x2 y2-z2
New General Mathematics for JSS Book3 pg29-34.
Further Studies
https://youtu.be/DjuNujTgL0E
https://youtu.be/TZWqkjraLWQ
https://youtu.be/lS9S1iEjlPI
WEEK 8
LESSON 26
TOPIC: Area and volume of cylinders and cones (Revision)
REFERENCE BOOK: New General Mathematics f or JS2, Page 184.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to calculate the surface area of a cylinder.
CONTENTS
Net of a cylinder
Area of upper surface = pie x r x r
Area of rectangle = L x B
But length = 2 pie x r
Breadth = h
The curved surface area = 2 pie x r x h
Example: A cylindrical cup has a circular base of radius 7cm and height of 10cm.
1. Calculate the area of its circular base.
2. The curved surface area.
Solution
Area of circular base
Pie = 22/7
R = 7cm
A = 22/7 x 7 x 7 = 154 square cm
Curved surface area = 2 pie x r x h
= 2 x 22/7 x 7 x 10
= 440 cm square
EXAMPLE 2
Calculate the curve surface area of a cylinder of diameter 58cm and height 86cm. Round your answer to 2 s f.
Curved Surface Area = 2 pie x r x h
Pie = 3.14
R = 58/2 = 29cm
H = 2 x 3.14 x 29 x 86
H = 15662.32
H = 16000 (2 s. f.)

EVALUATION:
1. A cylindrical cup has a circular base of radius 14cm and height 8cm. Calculate the area of its circular base.
Find the curved surface area.
2. Calculate the curved surface area of a cylinder of radius 30cm and height 36cm. Write your answer to 2 s f
ASSIGNMENT Answer questions 1b, 1c and 2 from New General Mathematics for JS2, Page 185, EX 19B.
further studies
http://www.youtube.com/watch?v=Tl_09zz072s
LESSON 27
TOPIC: Total Surface Area of a cylinder.
REFERENCE BOOK New General Mathematics for JS2, Page185.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to calculate the total surface area of a cylinder.

CONTENTS
Examples:
1. Calculate the total surface area of a cylinder with radius 7cm and height 30cm.
T. S. A. = 2 + 2
Pie = 22/7
R = 7cm 7
r = 7cm
H = 30cm
= (2 x 22/7 x 7 x 7) + (2 x 22/7 x 7 x 30)
= 308 + 1320
= 1628
Total surface area
(2 x 22/7 x 7 x 7) + (2 x 22/7 x 7 x 16)
= 308 + 704
= 1012

EVALUATION Calculate the total surface area of a cylinder with radius 10cmg and height 10cm.
(2) Find the total surface area of a cylinder with diameter 2cm and height 3cm.
ASSIGNMENT: Answer questions 6a and 6b from New General Mathematics 2, Page 185.
LESSON 28
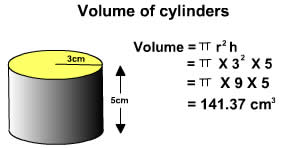
TOPIC: Volume of a cylinder.
REFERENCE BOOK: New General Mathematics f or JS2, Page186.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to calculate the volume of cylinders.
Image
CONTENTS
Volume of cylinder
Example: How many liters can be held by a cylindrical can 14cm in diameter and 20cm high.
Volume = 22/7 x 7 x 7 x20
Volume = 3080
Hint: 1 liter = 1000 cubic cm
Therefore capacity of the tank = 3080/1000
= 3.08 liters
EXAMPLE 2
The tank on a petrol lorry is a cylinder 8m in diameter and 7m long. Find its volume cubic meters.
VOLUME = 22/7 x 4 x 4 x 7
= 88 x 4
= 352
EVALUATION: Calculate the volume of a cylinder 8cm long and 3.5cm in diameter.
2. The tank on a petrol lorry is a cylinder 2m in diameter and 7m long.
(a) Calculate its volume in cubic meters.
(b) Find its capacity in kiloliters.
ASSIGNMENT Answer questions 3 and 5 from New General Mathematics 2, Page 187.
LESSON 29
TOPIC: Surface and total surface area of a cone
REFERENCE BOOK: New General Mathematics 2, Page188.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to find:
I. The surface area of a cone.
II. The total surface area of a cone.
CONTENTS: Curved Surface area of a cone

Curved Surface Area is the area of the sector = pie x r x l
Example: A cone has a base radius of 5cm and a slant height of 42cm. Find the curved surface area.
C. S. A. = 22/7 X 5 X 42
= 660
TOTAL SURFACE AREA
T. S. A = Pie x r x l + pie x r x r
EXAMPLE: Find the total surface area of a cone of slant height 10cm and base radius 5cm. (pie = 3.14)
Total surface area = (3.14 x 5 x 10) + (3.14 x 5 x 5)
= 157 + 78.5
= 235.5
Image
EVALUATION: A cone has a base radius of 3cm and a height of 4cm.
Calculate its slant height.
Find its surface area.
2. Calculate the total surface area of a cone of base radius 6cm and slant height 10cm
ASSIGNMENT: Answer questions 7c and 7d from New General Mathematics 2, Page 189.
LESSON 30
TOPIC: TOTAL SURFACE AREA OF A CONE
REFERENCES BOOK: New general maths for JSS 2, page 189
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the total surface area of a cone.
CONTENTS
Total surface area of a cone= ∏rl + ∏r2
Example:
Find the total surface area of a cone of slant height 10cm and base radius 5cm. (pie = 3.14)
Total surface area = (3.14 x 5 x 10) + (3.14 x 5 x 5)
= 157 + 78.5
= 235.5
EVALUATION
1. Calculate the total surface area of a cone of:
a. Base radius 6cm and slant height 10cm
b. Base radius 8cm and vertical height 6cm
ASSIGNMENT: New general maths for JSS 2 page 189. Nos 7c and 7d
LESSON 31
TOPIC: VOLUME OF A CONE
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the volume of cones.
View Content below

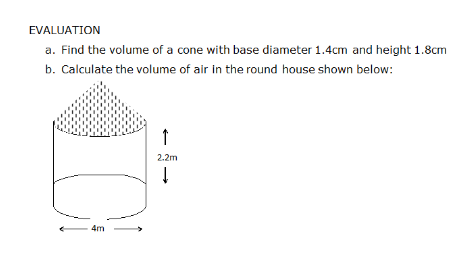
ASSIGNMENT: New general maths for JSS2, page 191 Nos 2 and 6
LESSON 32
TOPIC: CONES (Miscellaneous sums)
PERFORMANCE OBJECTIVE: At the end of the this lesson, students should be able to solve miscellaneous sums on surface area and volume of cones
View Content below

ASSIGNMENT: New general Maths for JSS2, page 191. Numbers 3 & 5
TOPIC: Area and volume of cylinders and cones (Revision)
REFERENCE BOOK: New General Mathematics f or JS2, Page 184.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to calculate the surface area of a cylinder.

CONTENTS
Net of a cylinder
Area of upper surface = pie x r x r
Area of rectangle = L x B
But length = 2 pie x r
Breadth = h
The curved surface area = 2 pie x r x h
Example: A cylindrical cup has a circular base of radius 7cm and height of 10cm.
1. Calculate the area of its circular base.
2. The curved surface area.
Solution
Area of circular base
Pie = 22/7
R = 7cm
A = 22/7 x 7 x 7 = 154 square cm
Curved surface area = 2 pie x r x h
= 2 x 22/7 x 7 x 10
= 440 cm square
EXAMPLE 2
Calculate the curve surface area of a cylinder of diameter 58cm and height 86cm. Round your answer to 2 s f.
Curved Surface Area = 2 pie x r x h
Pie = 3.14
R = 58/2 = 29cm
H = 2 x 3.14 x 29 x 86
H = 15662.32
H = 16000 (2 s. f.)

EVALUATION:
1. A cylindrical cup has a circular base of radius 14cm and height 8cm. Calculate the area of its circular base.
Find the curved surface area.
2. Calculate the curved surface area of a cylinder of radius 30cm and height 36cm. Write your answer to 2 s f
ASSIGNMENT Answer questions 1b, 1c and 2 from New General Mathematics for JS2, Page 185, EX 19B.
further studies
http://www.youtube.com/watch?v=Tl_09zz072s
LESSON 27
TOPIC: Total Surface Area of a cylinder.
REFERENCE BOOK New General Mathematics for JS2, Page185.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to calculate the total surface area of a cylinder.

CONTENTS
Examples:
1. Calculate the total surface area of a cylinder with radius 7cm and height 30cm.
T. S. A. = 2 + 2
Pie = 22/7
R = 7cm 7
r = 7cm
H = 30cm
= (2 x 22/7 x 7 x 7) + (2 x 22/7 x 7 x 30)
= 308 + 1320
= 1628
Total surface area
(2 x 22/7 x 7 x 7) + (2 x 22/7 x 7 x 16)
= 308 + 704
= 1012

EVALUATION Calculate the total surface area of a cylinder with radius 10cmg and height 10cm.
(2) Find the total surface area of a cylinder with diameter 2cm and height 3cm.
ASSIGNMENT: Answer questions 6a and 6b from New General Mathematics 2, Page 185.
LESSON 28
TOPIC: Volume of a cylinder.
REFERENCE BOOK: New General Mathematics f or JS2, Page186.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to calculate the volume of cylinders.
Image
CONTENTS
Volume of cylinder
Example: How many liters can be held by a cylindrical can 14cm in diameter and 20cm high.
Volume = 22/7 x 7 x 7 x20
Volume = 3080
Hint: 1 liter = 1000 cubic cm
Therefore capacity of the tank = 3080/1000
= 3.08 liters
EXAMPLE 2
The tank on a petrol lorry is a cylinder 8m in diameter and 7m long. Find its volume cubic meters.
VOLUME = 22/7 x 4 x 4 x 7
= 88 x 4
= 352

EVALUATION: Calculate the volume of a cylinder 8cm long and 3.5cm in diameter.
2. The tank on a petrol lorry is a cylinder 2m in diameter and 7m long.
(a) Calculate its volume in cubic meters.
(b) Find its capacity in kiloliters.
ASSIGNMENT Answer questions 3 and 5 from New General Mathematics 2, Page 187.
LESSON 29
TOPIC: Surface and total surface area of a cone
REFERENCE BOOK: New General Mathematics 2, Page188.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to find:
I. The surface area of a cone.
II. The total surface area of a cone.
CONTENTS: Curved Surface area of a cone

Curved Surface Area is the area of the sector = pie x r x l
Example: A cone has a base radius of 5cm and a slant height of 42cm. Find the curved surface area.
C. S. A. = 22/7 X 5 X 42
= 660
TOTAL SURFACE AREA
T. S. A = Pie x r x l + pie x r x r
EXAMPLE: Find the total surface area of a cone of slant height 10cm and base radius 5cm. (pie = 3.14)
Total surface area = (3.14 x 5 x 10) + (3.14 x 5 x 5)
= 157 + 78.5
= 235.5
Image
EVALUATION: A cone has a base radius of 3cm and a height of 4cm.
Calculate its slant height.
Find its surface area.
2. Calculate the total surface area of a cone of base radius 6cm and slant height 10cm
ASSIGNMENT: Answer questions 7c and 7d from New General Mathematics 2, Page 189.
LESSON 30
TOPIC: TOTAL SURFACE AREA OF A CONE
REFERENCES BOOK: New general maths for JSS 2, page 189
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the total surface area of a cone.
CONTENTS
Total surface area of a cone= ∏rl + ∏r2
Example:
Find the total surface area of a cone of slant height 10cm and base radius 5cm. (pie = 3.14)
Total surface area = (3.14 x 5 x 10) + (3.14 x 5 x 5)
= 157 + 78.5
= 235.5
EVALUATION
1. Calculate the total surface area of a cone of:
a. Base radius 6cm and slant height 10cm
b. Base radius 8cm and vertical height 6cm
ASSIGNMENT: New general maths for JSS 2 page 189. Nos 7c and 7d
LESSON 31
TOPIC: VOLUME OF A CONE
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the volume of cones.
View Content below


ASSIGNMENT: New general maths for JSS2, page 191 Nos 2 and 6
LESSON 32
TOPIC: CONES (Miscellaneous sums)
PERFORMANCE OBJECTIVE: At the end of the this lesson, students should be able to solve miscellaneous sums on surface area and volume of cones
View Content below

ASSIGNMENT: New general Maths for JSS2, page 191. Numbers 3 & 5
WEEK 9
LESSON 33
MAIN TOPIC: Charts and tables
SPECIFIC TOPIC: Reading tabulated Data.
PERFORMANCE OBJECTIVE: At the end of this person, students should be able to read and interpret tabulated data.
REFERENCE BOOK: New General Maths for JSS 2, page 178
CONTENTS
The table below is monthly rainfall chart from January of December.
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov
Sokoto 0 0 0 10 48 91 155 249 145 15 15
Jos 3 3 28 56 203 226 330 292 213 41 3
Ibadan 10 23 89 137 159 188 169 84 178 155 46
P-Harcourt 66 109 155 262 404 660 531 318 516 460 213
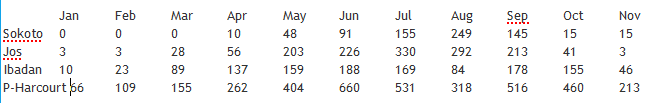
Use the table above to find the average rainfall for the following;
i. Sokoto in January 0mm
ii. Port-Harcourt in Dec 81
iii. Jos in May 203
iv. Ibadan in March 89
v. Sokoto in August 249
vi. Ibadan in July 160
vii. Jos in October 41
For each town, name the month which has the highest rainfall.
Sokoto = 249mm
Jos = 330mm
Ibadan = 188mm
P-Hacourt = 660mm
https://youtu.be/AZd9CdTU8XU
EVALUATION: New General Maths for JSS 2 page 176, table 18.2; question 1a - e
ASSIGNMENT: New general Maths for JSS2, page 176, questions 2a-e
LESSON 34
TOPIC: Graph of social environmental issues
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to read and interpret graph of social and environmental issues
REFERENCE BOOK: New general maths for JSS2, page 177
CONTENTS
Example: The table below shows the percentage of a sample of men and women living with HIV/AIDS who were able to access ARV drugs during the first 6months of their introduction
ACCESS TO ARV DRUGS
GENDER 1st month 2nd month 3rd month 4th month 5th month 6th month
Female 28% 48% 57% 69% 67% 83%
Male 24% 42% 43% 61% 64% 75%
a. In which month did the lowest % of people have ARV drugs.
b. In which month did the greatest % have ARV drugs.
c. Which of the two sexes appears to be more informed about ARV
d. What is the likely reason for the % increase over the period?
EVALUATION: New general maths for JSS 2, page 177; questions 6 & 9
LESSON 35
MAIN TOPIC: Time tables or charts
SPECIFIC TOPIC: Railway timetables
PERFORMANCE OBJECTIVE: At the end of their lesson, students should be able to read and interpret time tables of railways.
REFERENCE BOOK: New general maths for JSS 2, page 179
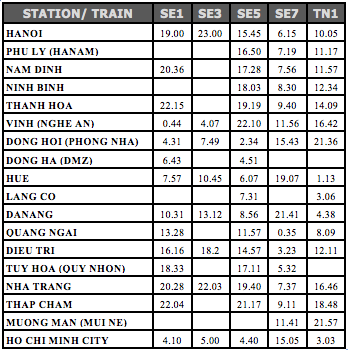
CONTENTS
The tables below is for train services between Ibadan and Offa
201 UP 202DN
IBADAN D 6:00PM A 11:30AM
OSHOGBO A 9:32PM D 7:58AM
D 9:42PM A 7:48AM
OFFA A D 6:00AM
UP up
DN down
a. What do the letters D and A stand for?
b. What time does the 201 UP train depart from Ibadan?
c. What time does the 201 UP train arrive in Offa?
d. How long does the 'up journey' take from Ibadan to Offa?
e. How long does the 201 up train stay at Oshogbo
EVALUATION
a. What time does the 202 DN train depart from Offa?
b. What time does the 202 DN train arrive at Ibadan?
c. How long does the ‘down journey’ take from Offa to Ibadan?
d. How long does the 202 DN train stay at Oshogbo?
ASSIGNMENT: New general maths for JSS2 page 179, Ex 18d: 1-10
further studies
Study More...
LESSON 36
TOPIC: The 24hrs clock
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to express 12hrs clock as 24hrs clock and vice versa.

View content below


https://youtu.be/f_n_KGf277I
https://youtu.be/ia6_4WXBFAw
ASSIGNMENT
Express the following as 24hrs clock.
(i) 5:30pm (ii) 10 past noon (iii) 3minutes past midnight (iv). 11:55pm
(v) 5mins to 9 at night
MAIN TOPIC: Charts and tables
SPECIFIC TOPIC: Reading tabulated Data.
PERFORMANCE OBJECTIVE: At the end of this person, students should be able to read and interpret tabulated data.
REFERENCE BOOK: New General Maths for JSS 2, page 178

CONTENTS
The table below is monthly rainfall chart from January of December.
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov
Sokoto 0 0 0 10 48 91 155 249 145 15 15
Jos 3 3 28 56 203 226 330 292 213 41 3
Ibadan 10 23 89 137 159 188 169 84 178 155 46
P-Harcourt 66 109 155 262 404 660 531 318 516 460 213
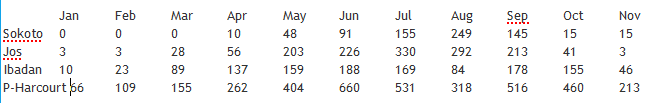
Use the table above to find the average rainfall for the following;
i. Sokoto in January 0mm
ii. Port-Harcourt in Dec 81
iii. Jos in May 203
iv. Ibadan in March 89
v. Sokoto in August 249
vi. Ibadan in July 160
vii. Jos in October 41
For each town, name the month which has the highest rainfall.
Sokoto = 249mm
Jos = 330mm
Ibadan = 188mm
P-Hacourt = 660mm
https://youtu.be/AZd9CdTU8XU
EVALUATION: New General Maths for JSS 2 page 176, table 18.2; question 1a - e
ASSIGNMENT: New general Maths for JSS2, page 176, questions 2a-e
LESSON 34
TOPIC: Graph of social environmental issues
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to read and interpret graph of social and environmental issues
REFERENCE BOOK: New general maths for JSS2, page 177
CONTENTS
Example: The table below shows the percentage of a sample of men and women living with HIV/AIDS who were able to access ARV drugs during the first 6months of their introduction
ACCESS TO ARV DRUGS
GENDER 1st month 2nd month 3rd month 4th month 5th month 6th month
Female 28% 48% 57% 69% 67% 83%
Male 24% 42% 43% 61% 64% 75%
a. In which month did the lowest % of people have ARV drugs.
b. In which month did the greatest % have ARV drugs.
c. Which of the two sexes appears to be more informed about ARV
d. What is the likely reason for the % increase over the period?

EVALUATION: New general maths for JSS 2, page 177; questions 6 & 9
LESSON 35
MAIN TOPIC: Time tables or charts
SPECIFIC TOPIC: Railway timetables
PERFORMANCE OBJECTIVE: At the end of their lesson, students should be able to read and interpret time tables of railways.
REFERENCE BOOK: New general maths for JSS 2, page 179

CONTENTS
The tables below is for train services between Ibadan and Offa
201 UP 202DN
IBADAN D 6:00PM A 11:30AM
OSHOGBO A 9:32PM D 7:58AM
D 9:42PM A 7:48AM
OFFA A D 6:00AM
UP up
DN down
a. What do the letters D and A stand for?
b. What time does the 201 UP train depart from Ibadan?
c. What time does the 201 UP train arrive in Offa?
d. How long does the 'up journey' take from Ibadan to Offa?
e. How long does the 201 up train stay at Oshogbo
EVALUATION
a. What time does the 202 DN train depart from Offa?
b. What time does the 202 DN train arrive at Ibadan?
c. How long does the ‘down journey’ take from Offa to Ibadan?
d. How long does the 202 DN train stay at Oshogbo?
ASSIGNMENT: New general maths for JSS2 page 179, Ex 18d: 1-10
further studies
Study More...
LESSON 36
TOPIC: The 24hrs clock
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to express 12hrs clock as 24hrs clock and vice versa.


View content below


https://youtu.be/f_n_KGf277I
https://youtu.be/ia6_4WXBFAw
ASSIGNMENT
Express the following as 24hrs clock.
(i) 5:30pm (ii) 10 past noon (iii) 3minutes past midnight (iv). 11:55pm
(v) 5mins to 9 at night