SCHEME OF WORK
WEEK TOPIC
1. Revision of first term examination questions.
2. Counting Base 2: counting in groups of twos: Addition of numbers in base 2 – Addition of two or three 3-digital binary numbers. Subtraction of numbers in Base 2 Numerals – subtraction of two 3-digital binary numbers.
3. Multiplication of Numbers in Base 2 Numerals: Multiplication of two 2-digit binary numbers. Solving problems on quantitative aptitude related to conversions and applications.
4. Addition and Subtraction: Revision on addition and subtraction of numbers with emphasis on place of value. Use of number line in illustrating directed numbers. Everyday application of positive and negative integers.
5. Addition and subtraction of positive and negative integers on the number line. Addition and subtraction of decimal fractions. Solving problems on quantitative reasoning in basic operations. The use of addition and subtraction in solving various life problems (fractions of percentages and percentages of fractions).
6. Algebraic Processes: Use of symbols. Open Sentences – solving problems expressed in open sentences. Appreciating the relationship between addition and subtraction, multiplication and division. Use of letters to represent symbols or shape in open sentences.
7. Algebraic Processes: use of symbols (cont’d): solving open sentences with two arithmetic operations. Solving world problems involving use of symbols. Solving quantitative aptitude (reasoning) problems on the use of symbols
8. Algebraic Processes – Identification of coefficients of terms, Basic arithmetic operations applied to expressions of similar terms. Collection and simplification of like terms, use of brackets.
9. Solving quantitative (reasoning) aptitude problems on the use of brackets. Word problems on the use of brackets. Word problems in symbolic terms.
10. Simple equations: translation of word problems into mathematical statements. Definition of simple equation and use of sign of equality in mathematical statements. Solution of simple equations.
11. Revision
2ND TERM
WEEK 1
LESSON 1
TOPIC Rounding off numbers
REFERENCE BOOKS New General Mathematics for West Africa 1 page
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to :
1 approximate numbers to the nearest ten
2 approximate numbers to the nearest hundred and thousand.
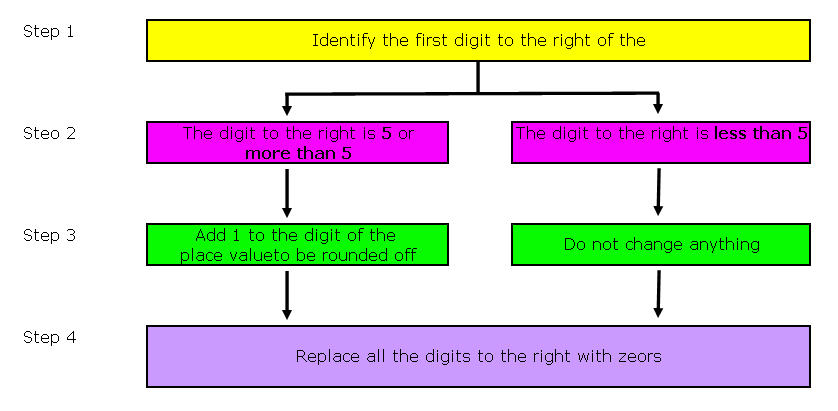
CONTENT
EXAMPLE: Approximate the following to the nearest ten:
1. 276 = 280
2. 14505 = 14510
Approximate the following to the nearest hundred :
1. 14505 =14500
2. 43891 =43900
Approximate the following to the nearest thousand :
1. 18624 = 19000 2. 9541 = 10000
EVALUATION Approximate the following to the nearest ten:
a. 81 b. 476 c. 32781
Approximate the following to the nearest thousand:
a. 2688 b.12505
ASSIGNMENT Round off the following to the nearest hundred:
a. 37916 b. 36352 c. 94618 d. 6227 e. 25847
rules & practice test
Further Studies 2
https://youtu.be/fd-E18EqSVk
LESSON 2
TOPIC Nearest whole number
REFERENCE BOOKS New General Mathematics for West Africa 1
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to approximate numbers to the nearest whole numbers.
CONTENTS
Rounding Decimals
27.17469 rounded to the nearest whole number is 27
36.74691 rounded to the nearest whole number is 37
12.34690 rounded to the nearest tenth is 12.3
89.46917 rounded to the nearest tenth is 89.5
50.02139 rounded to the nearest hundredth is 50.02
72.63539 rounded to the nearest hundredth is 72.64
46.83531 rounded to the nearest thousandth is 46.835
9.63967 rounded to the nearest thousandth is 9.640
Rules for rounding decimals.
1. Retain the correct number of decimal places (e.g. 3 for thousandths, 0 for whole numbers)
2. If the next decimal place value is 5 or more, increase the value in the last retained decimal place by 1.
Round off the following to the nearest whole numbers
1. 6.4 = 6
2. 28.5 = 29
3. 39.6 = 40
4. 2.48 = 2
5. 59.876 = 60
6. 0.7 = 1

EVALUATION Round off the following to the nearest whole numbers:
a. 3.55 b. 16.3 c. 99.56 d. 402.78 e. 0.88 f. 36.59 g. 9.6 h. 29.4 i. 78.75 j. 1.69 k. 4.09
ASSIGNMENT: Round off the following to the nearest whole numbers:
a. 26.45 b. 8.35 c. 5.84 d. 0.702 e. 3.08 f. 14.505 g. 8.54 h.79.75
Open Worksheet Here
https://youtu.be/9ZEUoGutPzM
LESSON 3
TOPIC Nearest tenth and hundredth
REFERENCE BOOKS New General Mathematics for West Africa 1 page 179.
BEHAVIOURAL OBJECTIVES: At the end of this lesson students should be able to;
1.round off numbers to the nearest tenth.
2.round off numbers to the nearest hundredth.
CONTENT
Nearest tenth:
a. 3.092 = 3.1 c. 8.226 = 8.2
b. 26.951 = 27.0
Nearest hundredth: a. 0.482 = 0.48 b. 2.736 = 2.74
c.0.266 = 0.27 d. 7999 = 8.00
EVALUATION: Round off to the nearest tenth:
a.0.71 b.0.45 c. 0.09 d.0.98 e. 0.15
Round off to the nearest hundredth:
a. 0.372 b. 0.155 c. 0.625 d. 0.097
ASSIGNMENT: Round off to the nearest thousandth:
a. 0.8416 b. 7.6599 c. 9.8231 d.25.5678 e. 0.0095
further studies
https://drive.google.com/file/d/0Bz3Mh6 ... sp=sharing
practice test
Practice Test
https://youtu.be/XnJw2wq930U
LESSON 4
TOPIC One significant figure
REFERENCE BOOKS New General Mathematics for West Africa , Page 179.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to:
1.round off numbers to one significant figure.
2.round off answers of given sums to one significant figure.
CONTENT
Round off the following to one significant figure:
a.47 =50 b. 0.275 c. 3.047 = 3.0
Round off each number to one significant figure, then approximate your answers;
a.57 + 31 = 60+ 30 90
b.291+ 603 = 300 + 600 = 900
c.4.2 +1.875 = 4 X 2 = 8
EVALUATION
Round off to one significant figure:
a.512 b.0.826 c. 7.56
Round off each number to one significant figure then approximate your answer: a.23+19 b 201- 77 c.653 - 287 d. 399X 95
ASSIGNMENT Round off each number to one significant figure and then approximate your answer:
a.17+58
b.9.774 / 4.62
c16.7 X 1.09
d.13.09 - 4.81
practice test
Practice Test
https://www.youtube.com/watch?v=6Qqzy4X-R2M
https://youtu.be/CGdBFY5sB_4
TOPIC Rounding off numbers
REFERENCE BOOKS New General Mathematics for West Africa 1 page
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to :
1 approximate numbers to the nearest ten
2 approximate numbers to the nearest hundred and thousand.

CONTENT
EXAMPLE: Approximate the following to the nearest ten:
1. 276 = 280
2. 14505 = 14510
Approximate the following to the nearest hundred :
1. 14505 =14500
2. 43891 =43900
Approximate the following to the nearest thousand :
1. 18624 = 19000 2. 9541 = 10000
EVALUATION Approximate the following to the nearest ten:
a. 81 b. 476 c. 32781
Approximate the following to the nearest thousand:
a. 2688 b.12505
ASSIGNMENT Round off the following to the nearest hundred:
a. 37916 b. 36352 c. 94618 d. 6227 e. 25847
rules & practice test
Further Studies 2
https://youtu.be/fd-E18EqSVk
LESSON 2
TOPIC Nearest whole number
REFERENCE BOOKS New General Mathematics for West Africa 1
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to approximate numbers to the nearest whole numbers.
CONTENTS
Rounding Decimals
27.17469 rounded to the nearest whole number is 27
36.74691 rounded to the nearest whole number is 37
12.34690 rounded to the nearest tenth is 12.3
89.46917 rounded to the nearest tenth is 89.5
50.02139 rounded to the nearest hundredth is 50.02
72.63539 rounded to the nearest hundredth is 72.64
46.83531 rounded to the nearest thousandth is 46.835
9.63967 rounded to the nearest thousandth is 9.640
Rules for rounding decimals.
1. Retain the correct number of decimal places (e.g. 3 for thousandths, 0 for whole numbers)
2. If the next decimal place value is 5 or more, increase the value in the last retained decimal place by 1.
Round off the following to the nearest whole numbers
1. 6.4 = 6
2. 28.5 = 29
3. 39.6 = 40
4. 2.48 = 2
5. 59.876 = 60
6. 0.7 = 1

EVALUATION Round off the following to the nearest whole numbers:
a. 3.55 b. 16.3 c. 99.56 d. 402.78 e. 0.88 f. 36.59 g. 9.6 h. 29.4 i. 78.75 j. 1.69 k. 4.09
ASSIGNMENT: Round off the following to the nearest whole numbers:
a. 26.45 b. 8.35 c. 5.84 d. 0.702 e. 3.08 f. 14.505 g. 8.54 h.79.75
Open Worksheet Here
https://youtu.be/9ZEUoGutPzM
LESSON 3
TOPIC Nearest tenth and hundredth
REFERENCE BOOKS New General Mathematics for West Africa 1 page 179.
BEHAVIOURAL OBJECTIVES: At the end of this lesson students should be able to;
1.round off numbers to the nearest tenth.
2.round off numbers to the nearest hundredth.
CONTENT
Nearest tenth:
a. 3.092 = 3.1 c. 8.226 = 8.2
b. 26.951 = 27.0
Nearest hundredth: a. 0.482 = 0.48 b. 2.736 = 2.74
c.0.266 = 0.27 d. 7999 = 8.00
EVALUATION: Round off to the nearest tenth:
a.0.71 b.0.45 c. 0.09 d.0.98 e. 0.15
Round off to the nearest hundredth:
a. 0.372 b. 0.155 c. 0.625 d. 0.097
ASSIGNMENT: Round off to the nearest thousandth:
a. 0.8416 b. 7.6599 c. 9.8231 d.25.5678 e. 0.0095
further studies
https://drive.google.com/file/d/0Bz3Mh6 ... sp=sharing
practice test
Practice Test
https://youtu.be/XnJw2wq930U
LESSON 4
TOPIC One significant figure
REFERENCE BOOKS New General Mathematics for West Africa , Page 179.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to:
1.round off numbers to one significant figure.
2.round off answers of given sums to one significant figure.
CONTENT
Round off the following to one significant figure:
a.47 =50 b. 0.275 c. 3.047 = 3.0
Round off each number to one significant figure, then approximate your answers;
a.57 + 31 = 60+ 30 90
b.291+ 603 = 300 + 600 = 900
c.4.2 +1.875 = 4 X 2 = 8
EVALUATION
Round off to one significant figure:
a.512 b.0.826 c. 7.56
Round off each number to one significant figure then approximate your answer: a.23+19 b 201- 77 c.653 - 287 d. 399X 95
ASSIGNMENT Round off each number to one significant figure and then approximate your answer:
a.17+58
b.9.774 / 4.62
c16.7 X 1.09
d.13.09 - 4.81
practice test
Practice Test
https://www.youtube.com/watch?v=6Qqzy4X-R2M
https://youtu.be/CGdBFY5sB_4
WEEK 2
LESSON 5
TOPIC Binary Numbers (Addition and Subtraction)
REFERENCE BOOK Macmillan Progressive Mathematics for JS1 Page 47.
BEHAVIOURAL OBJECTIVES:
At the end of this lesson, students should be able to add given binary numbers.
view content here
https://drive.google.com/file/d/1XyRku9 ... sp=sharing

EVALUATION The lesson is evaluated from Macmillan Progressive Mathematics for JS1 Page 47, Ex 5 QUESTIONS 1 - 5
ASSIGNMENT Macmillan Progressive Mathematics for JS1 ,Page 47, Ex 5, QUESTIONS 6 - 10
https://www.youtube.com/watch?v=sFd5bnDdB3Q
further studies
Further Studies
practice test
Practice Test
https://youtu.be/5F6orbqZigI
https://youtu.be/kTcpd4ef2lU
LESSON 6
TOPIC: COUNTING IN BASE 2
CONTENT:
Counting in groups of two
Addition of numbers in base two
Addition of two or three-digit binary numbers
Subtraction of Numbers in base 2
Subtraction of two or three-digit binary numbers
COUNTING IN GROUPS OF TWO
A number in base 2 is called a binary number. A binary number is a number that is made up of two digits – 0 and 1. If a number is written in base two, then none of its digits will exceed 1 in value; and its base should be indicated as a subscript. The base may be written in figure (numeral) or in word.
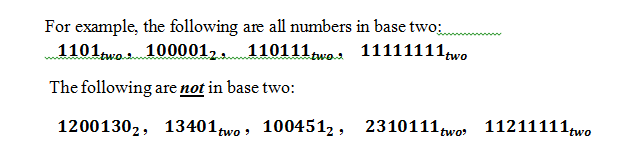
One of the rules of identifying numbers in base two is that none of its digit must be greater than 1. As we can see in the last five figures above, numbers like 2 , 3 , 4 , and 5 are embedded ( found ) in them. So, they are no more qualified to be in base two. All the digits of numbers written in base two must be only 0 and 1 throughout.
Once a digit is greater than 1 is found in any number, then that number is not in base 2. And the base of all numbers must be clarified or stated by its subscript. If the base is not indicated it is then simply assumed the number is in base ten or it is a common (ordinary) number.
Note:
Numbers written in base two are called BINARY numbers or we say base 2 numbers are in binary scale.
Numbers written in base eight are said to be in OCTAL scale.
Numbers written in base ten are said to be in DENARY or DECIMAL scale.
Numbers written in base twelve are said to be in DUODECIMAL scale.
Numbers written in base sixteen are said to be in HEXADECIMAL scale.
A binary number can be expressed as a sum of multiples of powers of two. In counting in group of twos, groups of two will be called whole or bundle while the remaining (remainder) is called units or ones.

https://youtu.be/Pr20m1zfuoA
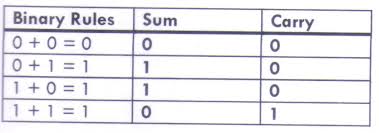
ADDITION OF BINARY NUMBERS
When adding binary numbers:
0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10
ADDITION OF TWO OR THREE DIGIT BINARY NUMBERS

https://youtu.be/5F6orbqZigI
SUBTRACTION OF NUMBERS IN BASE 2
When subtracting binary numbers:
0 – 0 = 0, 1 – 0 = 1 and 1 – 1 = 0

https://youtu.be/OHf0Eg9ZhGQ
READING ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Page 183 to 188
ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Ex. 24d Q2(a-l) to Q5, Page 187 to 188.
TOPIC Binary Numbers (Addition and Subtraction)
REFERENCE BOOK Macmillan Progressive Mathematics for JS1 Page 47.
BEHAVIOURAL OBJECTIVES:
At the end of this lesson, students should be able to add given binary numbers.

view content here
https://drive.google.com/file/d/1XyRku9 ... sp=sharing

EVALUATION The lesson is evaluated from Macmillan Progressive Mathematics for JS1 Page 47, Ex 5 QUESTIONS 1 - 5
ASSIGNMENT Macmillan Progressive Mathematics for JS1 ,Page 47, Ex 5, QUESTIONS 6 - 10
https://www.youtube.com/watch?v=sFd5bnDdB3Q
further studies
Further Studies
practice test
Practice Test
https://youtu.be/5F6orbqZigI
https://youtu.be/kTcpd4ef2lU
LESSON 6
TOPIC: COUNTING IN BASE 2
CONTENT:
Counting in groups of two
Addition of numbers in base two
Addition of two or three-digit binary numbers
Subtraction of Numbers in base 2
Subtraction of two or three-digit binary numbers
COUNTING IN GROUPS OF TWO
A number in base 2 is called a binary number. A binary number is a number that is made up of two digits – 0 and 1. If a number is written in base two, then none of its digits will exceed 1 in value; and its base should be indicated as a subscript. The base may be written in figure (numeral) or in word.
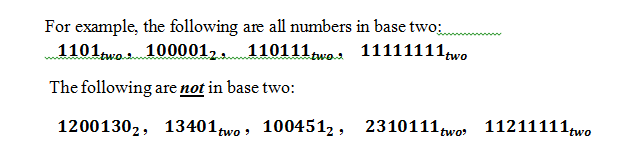
One of the rules of identifying numbers in base two is that none of its digit must be greater than 1. As we can see in the last five figures above, numbers like 2 , 3 , 4 , and 5 are embedded ( found ) in them. So, they are no more qualified to be in base two. All the digits of numbers written in base two must be only 0 and 1 throughout.
Once a digit is greater than 1 is found in any number, then that number is not in base 2. And the base of all numbers must be clarified or stated by its subscript. If the base is not indicated it is then simply assumed the number is in base ten or it is a common (ordinary) number.
Note:
Numbers written in base two are called BINARY numbers or we say base 2 numbers are in binary scale.
Numbers written in base eight are said to be in OCTAL scale.
Numbers written in base ten are said to be in DENARY or DECIMAL scale.
Numbers written in base twelve are said to be in DUODECIMAL scale.
Numbers written in base sixteen are said to be in HEXADECIMAL scale.
A binary number can be expressed as a sum of multiples of powers of two. In counting in group of twos, groups of two will be called whole or bundle while the remaining (remainder) is called units or ones.

https://youtu.be/Pr20m1zfuoA
ADDITION OF BINARY NUMBERS
When adding binary numbers:
0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10
ADDITION OF TWO OR THREE DIGIT BINARY NUMBERS

https://youtu.be/5F6orbqZigI
SUBTRACTION OF NUMBERS IN BASE 2
When subtracting binary numbers:
0 – 0 = 0, 1 – 0 = 1 and 1 – 1 = 0

https://youtu.be/OHf0Eg9ZhGQ
READING ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Page 183 to 188
ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Ex. 24d Q2(a-l) to Q5, Page 187 to 188.
WEEK 3
LESSON 7
TOPIC: Binary Numbers (Multiplication and Conversion)
REFERENCE BOOK: Macmillan Progressive Mathematics for JS1 Page 47.
BEHAVIOURAL OBJECTIVES:
At the end of this lesson, students should be able to multiply and convert given binary numbers.
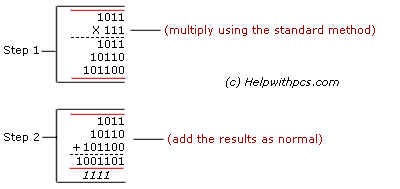
view content here
https://drive.google.com/file/d/1aMVN0i ... sp=sharing
further studies
http://www.binarymath.info/multiplication-division.php
LESSON 8
TOPIC: MULTIPLICATION OF NUMBERS IN BASE 2 NUMERALS
Multiplication of two 2-digit binary numbers.
Quantitative aptitude related to conversions and applications.
MULTIPLICATION OF 2-DIGIT BINARY NUMBERS.
We have studied addition and subtraction of numbers in binary system of counting, we can now proceed to the study of multiplication of numbers in base two.
To do this we need to know that:
(1). 0 x 0 = 0 (2). 0 x 1 = 0 (3). 1 x 1 = 1
Examples:
Multiply the followings leaving your answers in binary

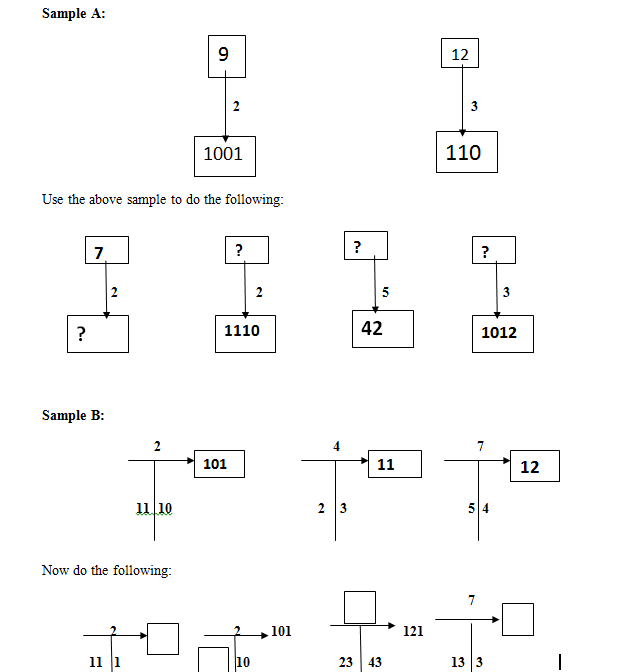
QUANTITATIVE APTITUDE REASONING ON NUMBER BASES
Sample A:
READING ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Page 184 to 188
ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Ex. 24d Q2(a-l) to Q5, Page 187 to 188.
https://youtu.be/Va_UvwJULcI
TOPIC: Binary Numbers (Multiplication and Conversion)
REFERENCE BOOK: Macmillan Progressive Mathematics for JS1 Page 47.
BEHAVIOURAL OBJECTIVES:
At the end of this lesson, students should be able to multiply and convert given binary numbers.

view content here
https://drive.google.com/file/d/1aMVN0i ... sp=sharing

further studies
http://www.binarymath.info/multiplication-division.php
LESSON 8
TOPIC: MULTIPLICATION OF NUMBERS IN BASE 2 NUMERALS
Multiplication of two 2-digit binary numbers.
Quantitative aptitude related to conversions and applications.
MULTIPLICATION OF 2-DIGIT BINARY NUMBERS.
We have studied addition and subtraction of numbers in binary system of counting, we can now proceed to the study of multiplication of numbers in base two.
To do this we need to know that:
(1). 0 x 0 = 0 (2). 0 x 1 = 0 (3). 1 x 1 = 1
Examples:
Multiply the followings leaving your answers in binary

QUANTITATIVE APTITUDE REASONING ON NUMBER BASES
Sample A:

READING ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Page 184 to 188
ASSIGNMENT:
New General Mathematics JS1 (UBE Edition), Ex. 24d Q2(a-l) to Q5, Page 187 to 188.
https://youtu.be/Va_UvwJULcI
WEEK 4
LESSON 9
TOPIC: Addition of numbers on the number line
REFERENCE BOOK: New General Mathematics f or JS1, Page 92.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to:
(1) Draw and use a number line to represent directed numbers (positive and negative numbers)
(2) Interpret and relate positive and negative numbers to everyday activities.

CONTENTS
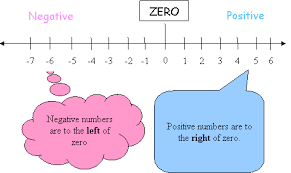
A number line is a picture of the counting numbers.
Use number line to solve: 1 + 4
-2 -1 0 1 2 3 4 5 6
EVALUATION: Use number lines to solve the following:
(a) 4+2
(b) 3 +4
(c) 4 - 1
(d) 7 -2
ASSIGNMENT: Use number lines to solve the following:
(a) 3 +5
(b) 5 + 7
(c) 4 - 7
(d) 9 - 3
further studies
https://www.mathsisfun.com/numbers/numb ... using.html
https://youtu.be/X4sRy7_usYI
LESSON 10
TOPIC: Addition and subtraction of positive numbers.
REFERENCE BOOK: New General Mathematics for JS1, Page 97.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to add subtract positive numbers.
CONTENTS
(a) -2 + 6 = +4 start from -2 move six steps to the right.
To add a positive number, move that number of places to the right on the number line.
(b) 3 - 7 = -4
To subtract a positive number, move that number of places to the left on the number line.
(c) Simplify: -3 -9 + 14
= 0 -3 -9 + 14 Start from -3, move nine steps to the left then fourteen steps to the right.
Thus, 0 - 3 -9 + 14 = +2
EVALUATION: Simplify:
(a) 6 - 7
(b) -3 + 1
(c) -5 -4
(d) -4 -6 + 12
ASSIGNMENT: Simplify:
(a) 7 - 15
(b) 12 - 17
(c) -3 -1
(d) 3 - 11 + 2
further studies
https://www.mathsteacher.com.au/year8/c ... tegers.htm
practice test
https://www.softschools.com/quizzes/mat ... z1034.html
https://www.mathsisfun.com/positive-neg ... egers.html
https://youtu.be/_BgblvF90UE
LESSON 11
TOPIC: Adding and Subtracting negative numbers.
REFERENCE BOOK: New General Mathematics f or JS1, Page 99.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to add and subtract negative numbers.
CONTENTS:
Subtracting Negative and Positive Integers
To subtract integers, change the sign on the integer that is to be subtracted.
If both signs are positive, the answer will be positive.
Example: 14 - (-6) = 14 + 6 = 20
If both signs are negative, the answer will be negative.
Example: -14 - (+6) = -14 - 6 = -20
If the signs are different subtract the smaller absolute value from the larger absolute value. The sign will be the sign of the integer that produced the larger absolute value.
Example: 14 - (+6) = 14 - 6 = 8
Example: -14 - (-6) = -14 + 6 = -8
To add a negative number : move that number of places to the left on the number line.
Example:
(a) 2 + (-5 )
= - 3
(b) - 3 + ( -3 )
= - 6
( c ) -3 + 14 + (- 5 ) = +6
To subtract a negative number, move that number of places to the right on the number line.
Example:
(a) 5 - (- 1 ) = 5 + 1 = 6
(b) (- 3 ) - ( - 1 ) = - 2
(c) 8 - (- 3 ) = 11
EVALUATION: Simplify:
(a) +4 + (-7 )
(b) -9 + - 9
(c) -3 + 14 + (- 5 )
(d) 0 + (- 5 )
(e) - 7 - ( -6 )
ASSIGNMENT: Solve the problems from New General Mathematics for JS1, Page 100, Ex 12i Questions 2 a - e
watch video
http://www.youtube.com/watch?v=eGtstF3kX6Q
LESSON 12
TOPIC: Positive and negative numbers in daily life.
REFERENCE BOOK New General Mathematics for JS1, Page 94.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to interpret and relate positive and negative numbers to everyday life.
CONTENTS
A map shows that the top of a hill is 200m above sea level and the bottom of a lagoon is 15m below sea- level.
(a) Give the positions of the bird and the fish as distances from the surface of the river.
(b) How far is the fish below the bird?
The bird is +200m (above sea level)
The fish is - 15m ( below sea level)
Zero hour for a meeting is midday ( 12 noon).
Express the following as positive or negative times.
(a) 4hour before zero hour. = - 4h
(b) 5 pm = + 5hrs.
(c) 30 mins before zero hr = -1/2hr
(d) 9 am = - 3hrs
EVALUATION: The lesson is evaluated from New General Mathematics for JS1, Page 95, Ex 12c, Questions 7g - i, 8,9.
further studies
https://drive.google.com/file/d/0Bz3Mh6 ... sp=sharing
https://youtu.be/OAoLCXpao6s
TOPIC: Addition of numbers on the number line
REFERENCE BOOK: New General Mathematics f or JS1, Page 92.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to:
(1) Draw and use a number line to represent directed numbers (positive and negative numbers)
(2) Interpret and relate positive and negative numbers to everyday activities.

CONTENTS
A number line is a picture of the counting numbers.
Use number line to solve: 1 + 4
-2 -1 0 1 2 3 4 5 6
EVALUATION: Use number lines to solve the following:
(a) 4+2
(b) 3 +4
(c) 4 - 1
(d) 7 -2
ASSIGNMENT: Use number lines to solve the following:
(a) 3 +5
(b) 5 + 7
(c) 4 - 7
(d) 9 - 3
further studies
https://www.mathsisfun.com/numbers/numb ... using.html
https://youtu.be/X4sRy7_usYI
LESSON 10
TOPIC: Addition and subtraction of positive numbers.
REFERENCE BOOK: New General Mathematics for JS1, Page 97.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to add subtract positive numbers.

CONTENTS
(a) -2 + 6 = +4 start from -2 move six steps to the right.
To add a positive number, move that number of places to the right on the number line.
(b) 3 - 7 = -4
To subtract a positive number, move that number of places to the left on the number line.
(c) Simplify: -3 -9 + 14
= 0 -3 -9 + 14 Start from -3, move nine steps to the left then fourteen steps to the right.
Thus, 0 - 3 -9 + 14 = +2
EVALUATION: Simplify:
(a) 6 - 7
(b) -3 + 1
(c) -5 -4
(d) -4 -6 + 12
ASSIGNMENT: Simplify:
(a) 7 - 15
(b) 12 - 17
(c) -3 -1
(d) 3 - 11 + 2
further studies
https://www.mathsteacher.com.au/year8/c ... tegers.htm
practice test
https://www.softschools.com/quizzes/mat ... z1034.html
https://www.mathsisfun.com/positive-neg ... egers.html
https://youtu.be/_BgblvF90UE
LESSON 11
TOPIC: Adding and Subtracting negative numbers.
REFERENCE BOOK: New General Mathematics f or JS1, Page 99.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to add and subtract negative numbers.
CONTENTS:
Subtracting Negative and Positive Integers
To subtract integers, change the sign on the integer that is to be subtracted.
If both signs are positive, the answer will be positive.
Example: 14 - (-6) = 14 + 6 = 20
If both signs are negative, the answer will be negative.
Example: -14 - (+6) = -14 - 6 = -20
If the signs are different subtract the smaller absolute value from the larger absolute value. The sign will be the sign of the integer that produced the larger absolute value.
Example: 14 - (+6) = 14 - 6 = 8
Example: -14 - (-6) = -14 + 6 = -8
To add a negative number : move that number of places to the left on the number line.
Example:
(a) 2 + (-5 )
= - 3
(b) - 3 + ( -3 )
= - 6
( c ) -3 + 14 + (- 5 ) = +6
To subtract a negative number, move that number of places to the right on the number line.
Example:
(a) 5 - (- 1 ) = 5 + 1 = 6
(b) (- 3 ) - ( - 1 ) = - 2
(c) 8 - (- 3 ) = 11
EVALUATION: Simplify:
(a) +4 + (-7 )
(b) -9 + - 9
(c) -3 + 14 + (- 5 )
(d) 0 + (- 5 )
(e) - 7 - ( -6 )
ASSIGNMENT: Solve the problems from New General Mathematics for JS1, Page 100, Ex 12i Questions 2 a - e
watch video
http://www.youtube.com/watch?v=eGtstF3kX6Q
LESSON 12
TOPIC: Positive and negative numbers in daily life.
REFERENCE BOOK New General Mathematics for JS1, Page 94.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to interpret and relate positive and negative numbers to everyday life.
CONTENTS
A map shows that the top of a hill is 200m above sea level and the bottom of a lagoon is 15m below sea- level.
(a) Give the positions of the bird and the fish as distances from the surface of the river.
(b) How far is the fish below the bird?
The bird is +200m (above sea level)
The fish is - 15m ( below sea level)
Zero hour for a meeting is midday ( 12 noon).
Express the following as positive or negative times.
(a) 4hour before zero hour. = - 4h
(b) 5 pm = + 5hrs.
(c) 30 mins before zero hr = -1/2hr
(d) 9 am = - 3hrs
EVALUATION: The lesson is evaluated from New General Mathematics for JS1, Page 95, Ex 12c, Questions 7g - i, 8,9.
further studies
https://drive.google.com/file/d/0Bz3Mh6 ... sp=sharing
https://youtu.be/OAoLCXpao6s
WEEK 5
LESSON 13
TOPIC: ADDITION AND SUBTRACTION OF NUMBERS
CONTENT:
Revision on addition and subtraction of numbers (place of value)
Use of number line in illustrating directed numbers.
Everyday application of positive and negative integers.
REVISION ON ADDITION AND SUBTRACTION OF NUMBERS (PLACE OF VALUE).
The place or position a particular digit occupies in a number shows its value.
The place value uses columns to show the size of each digit or figure in a number. Each column represents a different power of 10. So the place value of a digit increases by 10 times as it moves from the right to the left and decreases by 10 times as it moves from left to the right. Lets study the examples below.
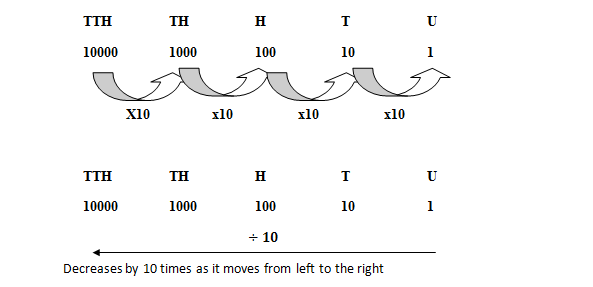
Where:
TTH = Tens of Thousands, TH = Thousands, H = Hundreds, T= Tens, U = Units
When a number is written out in its expanded form, the place value of digit becomes clearer. Example 38 952 in expanded form is
3×10000+8×1000+9×100+5×10+2×1
Example:
Find the place value of digit stand for in these numbers:
(a). 409 (b). 2440 (c). 798 005
Solutions:
. 409 : → 4 stands for 4 hundreds = 400
0 stands for 0 tens (i.e. no digit in this column) = 0
9 stands for 9units = 9
(b). 2440 :→ 2 stands for 2 thousands = 2000
4 stands for 4 hundreds = 400
stands for 4tens = 40
0 stands for 0 units (i.e. no digit in this column) = 0
(c). 798 005 : → 7 stands for 7 hundred thousands = 700 000
9 stands for 9 tens thousands = 90 000
8 stands for 8 thousands = 8 000
0 stands for 0hundreds (i.e. no digit in this column) = 0
0stands for 0 ten (i.e. no digit in this column) = 0
5stands for 5 ten = 5
ADDITION AND SUBTRACTION OF PLACE VALUE NUMBERS
Example:
Find the place value of each digit of the result of:
4567-1234 b. 23456 + 456789
Solutions:
4567-1234 = 3333: 1st 3 is thousands, 2nd 3 is hundreds, 3rd 3 is tens, 4th 3is units.
23456 + 456789 = 480 245 : 1st 4 is hundreds thousands, 8 is tens thousands, 0 is thousands, 2 is hundreds, 2nd 4 is tens, 5 is units.

EVERYDAY APPLICATION OF POSITIVE AND NEGATIVE INTEGERS.
Both negative and positive numbers are useful in everyday life affairs.
Examples:
1. Temperature reading e.g -70C, 500C, etc
2. Financial system: Gain is represented by positive numbers while Loss is denoted by negative numbers e.g. -$70, $56, etc
3. Distance above and below ground level: above (+) and below (-)
4. Time differences in different part of the world are also measured using negative and positive numbers.
EVALUATION:
1. In each of the following numbers, what does the digit 5 stands for?
(a) 7500 (b). 176501 (c). 3875 (d). 3759
2. Evaluate the following and write out the place value of the results.
(a). 16789 + 437562 (b). 8506 – 4408 (c). 6526 – 2314 (d). 421563 + 21037
3. Mention five applications of integers in our day today living.
READING ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS1 (UBE Edition), Page 92 to 99
ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS1 (UBE Edition), Ex. 12c Q1 to Q18, Page 95 to 96.
https://youtu.be/_BgblvF90UE
https://youtu.be/K_tPbVPfHgk
TOPIC: ADDITION AND SUBTRACTION OF NUMBERS
CONTENT:
Revision on addition and subtraction of numbers (place of value)
Use of number line in illustrating directed numbers.
Everyday application of positive and negative integers.
REVISION ON ADDITION AND SUBTRACTION OF NUMBERS (PLACE OF VALUE).
The place or position a particular digit occupies in a number shows its value.
The place value uses columns to show the size of each digit or figure in a number. Each column represents a different power of 10. So the place value of a digit increases by 10 times as it moves from the right to the left and decreases by 10 times as it moves from left to the right. Lets study the examples below.

Where:
TTH = Tens of Thousands, TH = Thousands, H = Hundreds, T= Tens, U = Units
When a number is written out in its expanded form, the place value of digit becomes clearer. Example 38 952 in expanded form is
3×10000+8×1000+9×100+5×10+2×1
Example:
Find the place value of digit stand for in these numbers:
(a). 409 (b). 2440 (c). 798 005
Solutions:
. 409 : → 4 stands for 4 hundreds = 400
0 stands for 0 tens (i.e. no digit in this column) = 0
9 stands for 9units = 9
(b). 2440 :→ 2 stands for 2 thousands = 2000
4 stands for 4 hundreds = 400
stands for 4tens = 40
0 stands for 0 units (i.e. no digit in this column) = 0
(c). 798 005 : → 7 stands for 7 hundred thousands = 700 000
9 stands for 9 tens thousands = 90 000
8 stands for 8 thousands = 8 000
0 stands for 0hundreds (i.e. no digit in this column) = 0
0stands for 0 ten (i.e. no digit in this column) = 0
5stands for 5 ten = 5
ADDITION AND SUBTRACTION OF PLACE VALUE NUMBERS
Example:
Find the place value of each digit of the result of:
4567-1234 b. 23456 + 456789
Solutions:
4567-1234 = 3333: 1st 3 is thousands, 2nd 3 is hundreds, 3rd 3 is tens, 4th 3is units.
23456 + 456789 = 480 245 : 1st 4 is hundreds thousands, 8 is tens thousands, 0 is thousands, 2 is hundreds, 2nd 4 is tens, 5 is units.

EVERYDAY APPLICATION OF POSITIVE AND NEGATIVE INTEGERS.
Both negative and positive numbers are useful in everyday life affairs.
Examples:
1. Temperature reading e.g -70C, 500C, etc
2. Financial system: Gain is represented by positive numbers while Loss is denoted by negative numbers e.g. -$70, $56, etc
3. Distance above and below ground level: above (+) and below (-)
4. Time differences in different part of the world are also measured using negative and positive numbers.
EVALUATION:
1. In each of the following numbers, what does the digit 5 stands for?
(a) 7500 (b). 176501 (c). 3875 (d). 3759
2. Evaluate the following and write out the place value of the results.
(a). 16789 + 437562 (b). 8506 – 4408 (c). 6526 – 2314 (d). 421563 + 21037
3. Mention five applications of integers in our day today living.
READING ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS1 (UBE Edition), Page 92 to 99
ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS1 (UBE Edition), Ex. 12c Q1 to Q18, Page 95 to 96.
https://youtu.be/_BgblvF90UE
https://youtu.be/K_tPbVPfHgk
WEEK 6
LESSON 14
TOPIC: ALGEBRAIC PROCESSES: USE OF SYMBOLS
CONTENT:
Open sentences
Appreciating the relationship between addition and subtraction
Multiplication and division
Use of letters to represent symbols or shape in open sentences.
OPEN SENTENCES

EVALUATION:
Each sentence is true, find the number which makes it true.
(1). X = 2+9 (2). Y = 9+ 5 (3) q x q = 4 (4). h x 4 = 20 (5) z – 6 = 2 (6) g+ g = 30
https://youtu.be/dAgfnK528RA
READING ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS 1 UBE EDITION, pg 40- 43.
ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS 1 UBE EDITION, pg 40- 41.
EX. 5a 51-60; 5b 7-10; 5c. 1( a-e)
LESSON 15
TOPIC: ALGEBRAIC PROCESSES: USE OF SYMBOLS
CONTENT:
Solving open sentences with two arithmetic operations
Solving world problems involving use of symbols.
Quantitative Aptitude (reasoning) on the use of symbols
SOLVING WORLD PROBLEMS INVOLVING USE OF SYMBOLS
Here we use letters of the alphabet to represent objects. First we need to know the following basics:
The other names for addition are sum, plus, increase, etc.
The other names for subtraction are difference, minus, decrease, remove,..
The other names for multiplication are product, times, double, triple, etc. For instance: Twice x=2x; Double y=y+y=2y;
Tripple x=3x .
The other names for Division are quotient, half, one-third, one-fourth, one-fifth, etc.
Students to study the illustrations in the table below:

Examples:
Write the algebraic expressions for the following verbal statements. Twice a number added to 18 is 84.
Answer: 2x+18=84.
Triple a number subtracted from 19 is – 12.
Answer: 19-3x=-12.
Sum of 5 and a number equals twice the number subtracted from 1. Answer: 5+x=1-2x .
Four times a number added to itself is 50.
Answer is 4y+y=50.
A number is twice another number. If their sum is 12, find the number.
Answer: 2x+x=12. ⟹ 3x=12. ⟹3(x)=12.
⟹3(4)=12. ∴ x=4.
EVALUATION:
Write the algebraic expression for each of the following verbal statements.
Twice a number subtracted from 37 is 19.
A number added to five times itself gives 45.
One –third of a number added to its half is 8.
The difference of 56 and a number is 22.
A girl is 14 years old, how old will she be in x years time?
A boy is 15 years old, how old was he x years ago?
QUANTITATIVE APTITUDE REASONING ON THE USE OF SYMBOLS
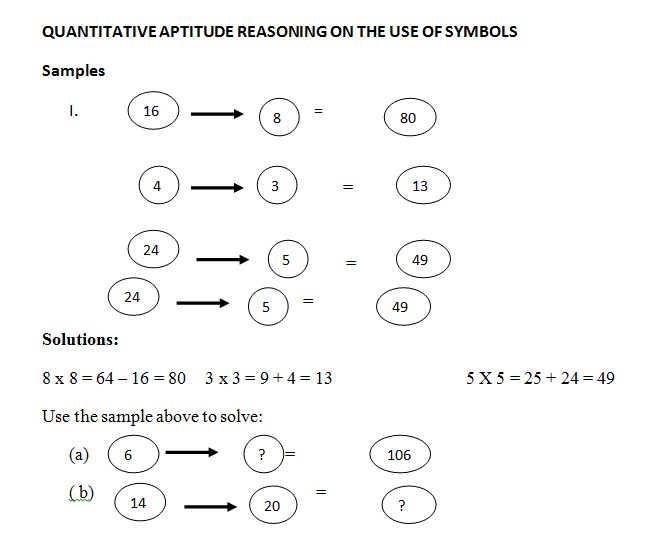
https://youtu.be/NybHckSEQBI
TOPIC: ALGEBRAIC PROCESSES: USE OF SYMBOLS
CONTENT:
Open sentences
Appreciating the relationship between addition and subtraction
Multiplication and division
Use of letters to represent symbols or shape in open sentences.
OPEN SENTENCES

EVALUATION:
Each sentence is true, find the number which makes it true.
(1). X = 2+9 (2). Y = 9+ 5 (3) q x q = 4 (4). h x 4 = 20 (5) z – 6 = 2 (6) g+ g = 30
https://youtu.be/dAgfnK528RA
READING ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS 1 UBE EDITION, pg 40- 43.
ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS 1 UBE EDITION, pg 40- 41.
EX. 5a 51-60; 5b 7-10; 5c. 1( a-e)
LESSON 15
TOPIC: ALGEBRAIC PROCESSES: USE OF SYMBOLS
CONTENT:
Solving open sentences with two arithmetic operations
Solving world problems involving use of symbols.
Quantitative Aptitude (reasoning) on the use of symbols
SOLVING WORLD PROBLEMS INVOLVING USE OF SYMBOLS
Here we use letters of the alphabet to represent objects. First we need to know the following basics:
The other names for addition are sum, plus, increase, etc.
The other names for subtraction are difference, minus, decrease, remove,..
The other names for multiplication are product, times, double, triple, etc. For instance: Twice x=2x; Double y=y+y=2y;
Tripple x=3x .
The other names for Division are quotient, half, one-third, one-fourth, one-fifth, etc.
Students to study the illustrations in the table below:

Examples:
Write the algebraic expressions for the following verbal statements. Twice a number added to 18 is 84.
Answer: 2x+18=84.
Triple a number subtracted from 19 is – 12.
Answer: 19-3x=-12.
Sum of 5 and a number equals twice the number subtracted from 1. Answer: 5+x=1-2x .
Four times a number added to itself is 50.
Answer is 4y+y=50.
A number is twice another number. If their sum is 12, find the number.
Answer: 2x+x=12. ⟹ 3x=12. ⟹3(x)=12.
⟹3(4)=12. ∴ x=4.
EVALUATION:
Write the algebraic expression for each of the following verbal statements.
Twice a number subtracted from 37 is 19.
A number added to five times itself gives 45.
One –third of a number added to its half is 8.
The difference of 56 and a number is 22.
A girl is 14 years old, how old will she be in x years time?
A boy is 15 years old, how old was he x years ago?
QUANTITATIVE APTITUDE REASONING ON THE USE OF SYMBOLS

https://youtu.be/NybHckSEQBI
WEEK 7
LESSON 16
TOPIC: ALGEBRAIC PROCESSES
CONTENT:
Identification of coefficients of terms
Basic arithmetic operations applied to expressions of similar terms
Collection and simplification of like terms
use of brackets
IDENTIFICATION OF COEFFICIENTS OF TERMS
We all know that terms like 3a, 4b, 3y +2, 5t + 6 etc are called algebraic expressions; also 3 in 3a, 4 in 4b, 3 in 3y and 5 in 5t are all called coefficients.
The coefficient can also be in fractions like 7/8 x,2/3 y,1/2 t , the coefficient is as follows: 7/8,2/3,1/2 respectively.
OR
In decimal like 0.5a, 0.25b and the coefficient are 0.5 and 0.25 respectively.

EVALUATION:
Give the coefficient of each of the following terms:
6t 2. 5/8 g 3. 0.35y
https://youtu.be/DBV-R5it_Kw
BASIC ARITHMETIC OPERATIONS APPLIED TO EXPRESSIONS OF SIMILAR TERMS
In algebraic expressions we can have positive and negative terms which can be added to produce another term.
Examples:
Simplify the following:
(a) 3y +2y = 5y (b) 4x + 3x = 7x (c ) 8t-3t + 4t -2t =8t + 4t -3t-2t = 12t-5t = 7t
EVALUATION:
Simplify the following:
21x – 7x
32x + 21x
8y+7y-9y-4y-2y
https://youtu.be/aR6phzMLuKM
COLLECTION AND SIMPLIFICATION OF LIKE TERMS
Algebraic expression such as 2a and 3a are called like terms because they are expressed in terms of a single variable a. If we take 2a and 3b, they are not like terms because they are not represented by a single term. So they are unlike terms.
In simplification of algebraic expressions, like and unlike terms are collected (grouped) together.
Examples:
Simplify the following expressions:
3x + 8x – 36 = 11x -36
8d -3d +4e-2e = 11d -2e
Examples:
In a box there are 12 socks and 6 shoes. In another box there are 4 socks and 8 shoes. Write down these statements using x for socks and y for shoes.
Solution:
In the first box we have 12x+6y , and in the second box we have4x+8y. Thus, total = 16x+14y.
A mother’s age is four times as old as her son’s and the sum of their ages is now 60 years. Write down the statement in symbol forms and find their ages.
Solution: If the son’s age is represented with letter x. Then the mother is (4×x) years old or 4x years old. Sum of their ages equals 60 years ⟹ 4x+x=60. ⟹5x=60. ⟹5(12)=60.
The son is 12 years old and the mother is 4×x = 4×12=48 years of age.
Now a man’s age is three times the son’s age. Five years ago the man’s age was five times the son’s age. Write down the algebraic expression for this word problem and possibly find the unknown.
Solution:
Let the son’s age be y. His father’s age at the present =3y. 5 years ago, the son’s age was (y-5)years and the father’s age was (3y-5)years.
At that time (five years ago), father’s age = 5 (son’s age).
⟹ (3y-5)=5 (y-5) .
⟹3y-5=5y-25⟹3y-5y=-25+5⟹-2y=-20⟹y=(-20)/(-10)=2
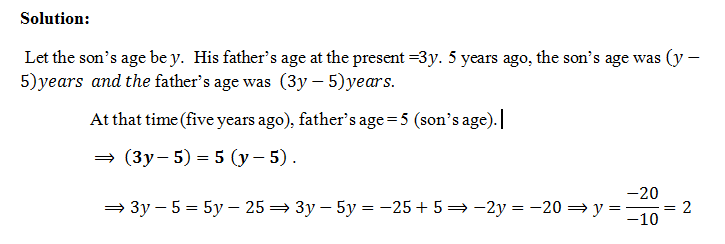
EVALUATION:
John has 12 apples more than Joel. If the sum of their apples is 49, how many apples have Joel and how many apples has John?
A girl guesses that a line is 15cm long. She measures the line and finds that her guess is x cm too long. What is the length of the line?
A boy is m years old now, how old will he be in 8 years time?. How old was he six years ago?
https://youtu.be/8GOo6QsFAEU
LESSON 17
USE OF BRACKETS, EXPANSION / REMOVAL OF BRACKETS IN (SIMPLE CASES).
The symbols for brackets are commonly ( ) , [ ], or { },
As shown here, the first are called curved brackets, the second box brackets and the third type are referred to as Curly brackets. Algebraic expressions could be put inside the brackets. For instance we could have (5n+4h) , [7x-2e], or {x-2y+z-5}. Bracket could be seen as Multiplication when there is a numeral or a letter written outside it , and also when a negative(minus) sign is preceding it.
For example if we have 3(2x-9) , it is intended that the 3 outside the brackets is to multiply through each term in the brackets. In other words 3 will multiply 2x and also multiply -9 , one after the other. When these multiplication operations are carried out correctly we say we have expanded or opened or removed the brackets. Thus we can remove or expand the brackets in the example below:
3(2x-9) = 3×2x-3×9 = 6x-27. Here, when the brackets in 3(2x-9) are opened
we have the final result as 6x-27. What it actually means is that 3(2x-9) and 6x-27 are equivalent.
However, there are two basic rules which guide how we open or expand brackets:
Any bracket preceded by a negative number or by a negative sign will have all the signs of its contents changed after the operation.
Examples:
-2(5x-8)=-10x+16.
-(-6y+h )=6y-h.
-{-4d-3x}=4d+3x.
-10(m+2w)=-10m-20w.
Any bracket preceded by a positive number or by a positive sign will have all the signs of its contents unchanged after the operation.
Examples:
2(5x-8)=10x-16 .
(-6y+h )=-6y+h .
{-4d-3x}=-4d-3x.
10(m+2w)=10m+20w.
+(5f-8g)=5f-8g .
+(2n+9k)=2n+9k .
Examples:
Expand the brackets and simplify further as far as possible, in the algebraic expression -5(4y+2m-3)-(3y-4m+6).
Solution:
-5(4y+2m-3)-(3y-4m+6). = -20y-10m+15-3y+4m-6 .
= -20y-3y-10m+4m+15-6 (by collecting like-terms together).
= -23y-6m+9. (This is the final result).
Expand the brackets and simplify further as far as possible, in the algebraic expression
7(4a-5b+c)-6(-3a-b+5c).
= 7(4a-5b+c)-6(-3a-b+5c).
=28a-35b+7c+18a+6b-30c.
=28a+18a+6b-35b+7c-30c.
=46a-29b-23c. (This is the final result).
EVALUATION:
Open the brackets in the following and simplify as far as possible.
(a).-(12y+8m-5)-(8y-m+7). (b).5(x+6y-4z)-(3x+2z-6y).
https://youtu.be/QXE8W-AD8pw
https://youtu.be/ZILVUNImJIE
READING ASSIGNMENT:
New General Mathematics for Junior Secondary Schools 1 (UBE EDITION) Pages 124 – 129.
ASSIGNMENT:
New General Mathematics for Junior Secondary Schools 1 (EDITION) Pages 124 – 129. EX. 15a (27-30); 15b (27-30); 15c (7-10); 15d (7-10);
TOPIC: ALGEBRAIC PROCESSES
CONTENT:
Identification of coefficients of terms
Basic arithmetic operations applied to expressions of similar terms
Collection and simplification of like terms
use of brackets
IDENTIFICATION OF COEFFICIENTS OF TERMS
We all know that terms like 3a, 4b, 3y +2, 5t + 6 etc are called algebraic expressions; also 3 in 3a, 4 in 4b, 3 in 3y and 5 in 5t are all called coefficients.
The coefficient can also be in fractions like 7/8 x,2/3 y,1/2 t , the coefficient is as follows: 7/8,2/3,1/2 respectively.
OR
In decimal like 0.5a, 0.25b and the coefficient are 0.5 and 0.25 respectively.

EVALUATION:
Give the coefficient of each of the following terms:
6t 2. 5/8 g 3. 0.35y
https://youtu.be/DBV-R5it_Kw
BASIC ARITHMETIC OPERATIONS APPLIED TO EXPRESSIONS OF SIMILAR TERMS
In algebraic expressions we can have positive and negative terms which can be added to produce another term.
Examples:
Simplify the following:
(a) 3y +2y = 5y (b) 4x + 3x = 7x (c ) 8t-3t + 4t -2t =8t + 4t -3t-2t = 12t-5t = 7t
EVALUATION:
Simplify the following:
21x – 7x
32x + 21x
8y+7y-9y-4y-2y
https://youtu.be/aR6phzMLuKM
COLLECTION AND SIMPLIFICATION OF LIKE TERMS
Algebraic expression such as 2a and 3a are called like terms because they are expressed in terms of a single variable a. If we take 2a and 3b, they are not like terms because they are not represented by a single term. So they are unlike terms.
In simplification of algebraic expressions, like and unlike terms are collected (grouped) together.
Examples:
Simplify the following expressions:
3x + 8x – 36 = 11x -36
8d -3d +4e-2e = 11d -2e
Examples:
In a box there are 12 socks and 6 shoes. In another box there are 4 socks and 8 shoes. Write down these statements using x for socks and y for shoes.
Solution:
In the first box we have 12x+6y , and in the second box we have4x+8y. Thus, total = 16x+14y.
A mother’s age is four times as old as her son’s and the sum of their ages is now 60 years. Write down the statement in symbol forms and find their ages.
Solution: If the son’s age is represented with letter x. Then the mother is (4×x) years old or 4x years old. Sum of their ages equals 60 years ⟹ 4x+x=60. ⟹5x=60. ⟹5(12)=60.
The son is 12 years old and the mother is 4×x = 4×12=48 years of age.
Now a man’s age is three times the son’s age. Five years ago the man’s age was five times the son’s age. Write down the algebraic expression for this word problem and possibly find the unknown.
Solution:
Let the son’s age be y. His father’s age at the present =3y. 5 years ago, the son’s age was (y-5)years and the father’s age was (3y-5)years.
At that time (five years ago), father’s age = 5 (son’s age).
⟹ (3y-5)=5 (y-5) .
⟹3y-5=5y-25⟹3y-5y=-25+5⟹-2y=-20⟹y=(-20)/(-10)=2
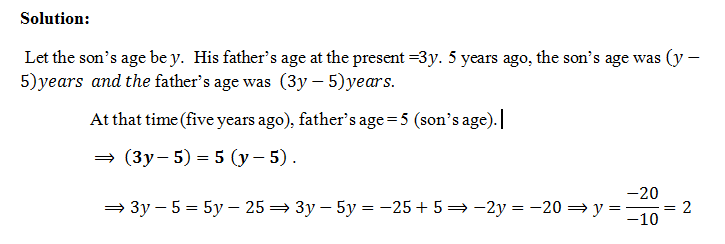
EVALUATION:
John has 12 apples more than Joel. If the sum of their apples is 49, how many apples have Joel and how many apples has John?
A girl guesses that a line is 15cm long. She measures the line and finds that her guess is x cm too long. What is the length of the line?
A boy is m years old now, how old will he be in 8 years time?. How old was he six years ago?
https://youtu.be/8GOo6QsFAEU
LESSON 17
USE OF BRACKETS, EXPANSION / REMOVAL OF BRACKETS IN (SIMPLE CASES).
The symbols for brackets are commonly ( ) , [ ], or { },
As shown here, the first are called curved brackets, the second box brackets and the third type are referred to as Curly brackets. Algebraic expressions could be put inside the brackets. For instance we could have (5n+4h) , [7x-2e], or {x-2y+z-5}. Bracket could be seen as Multiplication when there is a numeral or a letter written outside it , and also when a negative(minus) sign is preceding it.
For example if we have 3(2x-9) , it is intended that the 3 outside the brackets is to multiply through each term in the brackets. In other words 3 will multiply 2x and also multiply -9 , one after the other. When these multiplication operations are carried out correctly we say we have expanded or opened or removed the brackets. Thus we can remove or expand the brackets in the example below:
3(2x-9) = 3×2x-3×9 = 6x-27. Here, when the brackets in 3(2x-9) are opened
we have the final result as 6x-27. What it actually means is that 3(2x-9) and 6x-27 are equivalent.
However, there are two basic rules which guide how we open or expand brackets:
Any bracket preceded by a negative number or by a negative sign will have all the signs of its contents changed after the operation.
Examples:
-2(5x-8)=-10x+16.
-(-6y+h )=6y-h.
-{-4d-3x}=4d+3x.
-10(m+2w)=-10m-20w.
Any bracket preceded by a positive number or by a positive sign will have all the signs of its contents unchanged after the operation.
Examples:
2(5x-8)=10x-16 .
(-6y+h )=-6y+h .
{-4d-3x}=-4d-3x.
10(m+2w)=10m+20w.
+(5f-8g)=5f-8g .
+(2n+9k)=2n+9k .
Examples:
Expand the brackets and simplify further as far as possible, in the algebraic expression -5(4y+2m-3)-(3y-4m+6).
Solution:
-5(4y+2m-3)-(3y-4m+6). = -20y-10m+15-3y+4m-6 .
= -20y-3y-10m+4m+15-6 (by collecting like-terms together).
= -23y-6m+9. (This is the final result).
Expand the brackets and simplify further as far as possible, in the algebraic expression
7(4a-5b+c)-6(-3a-b+5c).
= 7(4a-5b+c)-6(-3a-b+5c).
=28a-35b+7c+18a+6b-30c.
=28a+18a+6b-35b+7c-30c.
=46a-29b-23c. (This is the final result).
EVALUATION:
Open the brackets in the following and simplify as far as possible.
(a).-(12y+8m-5)-(8y-m+7). (b).5(x+6y-4z)-(3x+2z-6y).
https://youtu.be/QXE8W-AD8pw
https://youtu.be/ZILVUNImJIE
READING ASSIGNMENT:
New General Mathematics for Junior Secondary Schools 1 (UBE EDITION) Pages 124 – 129.
ASSIGNMENT:
New General Mathematics for Junior Secondary Schools 1 (EDITION) Pages 124 – 129. EX. 15a (27-30); 15b (27-30); 15c (7-10); 15d (7-10);
WEEK 8
LESSON 18
TOPIC: Removing Brackets.
REFERENCE BOOK: New General Mathematics f or JS1, Page 127.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to remove brackets from simple numerical and algebraic expressions.
CONTENTS
Positive sign before a bracket: When there is a positive sign before a bracket, the signs inside the bracket remain the same.
Simplify: 7g + (3g + 4h)
= 7g + 3g + 4h
= 10g + 4h.
Simplify: 13p + (6p - 3p)
= 13p + 6p - 3p
= 19p - 3p
= 16p.
Simplify: (6x - 5y) + (3y + 4x)
= 6x - 5y + 3y + 4x
= 6x + 4x +3y - 5y = 10x - 2y
EVALUATION: The lesson is evaluated from New General Mathematics for JS1, Page 127, Ex. 15g, Questions 9 -12.
ASSIGNMENT: Answer questions 13, 14 and 15 from new General Mathematics for JS1, Page 127 Ex. 15g.
further studies
http://www.mathsisfun.com/algebra/expanding.html
https://youtu.be/v-6MShC82ow
LESSON19
TOPIC: Removing brackets: Negative sign before a bracket.
REFERENCE BOOK: New General Mathematics for JS1, Page127.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to remove brackets from expressions having negative signs before the brackets.
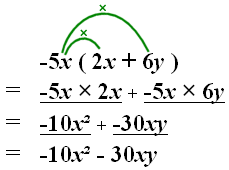
CONTENTS
Examples:
Simplify:
(a)
= 5a - (2a + 8 )
= 5a - 2a - 8
= 3a - 8.
In general, when there is a negative sign before a bracket: the signs of the terms inside the bracket are changed when the bracket is removed.
(b) Simplify:
10d - (9c - 4d)
= 10d - 9c + 4d
= 10d + 4d - 9c
= 14d - 9c.
(C ) Simplify:
(6x - y ) - (7x- 2y)
= 6x - y - 7x + 2y
= 6x - 7x + 2y - y
= -x + y or y - x .
EVALUATION: Remove brackets from the following and then simplify:
(a) 3a - (a + 5)
(b) 5x - (2 - x)
(c) (14x + 5y) - (7x - 6y)
(d) (8x + 3y)- (4x + y).
ASSIGNMENT: Answer questions 10 - 12 of exercise 15j, Page128 from New General Mathematics for JS1.
further studies
http://www.themathpage.com/alg/parentheses.htm
http://www.math-only-math.com/removal-of-brackets.html
https://youtu.be/LDIiYKYvvdA
LESSON 20
TOPIC: Algebraic Simplification: (Word Problems)
REFERENCE BOOK: New General Mathematics f or JS1, Page128.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve word problems on algebraic simplification.

CONTENTS
Example: A pen costs x naira and a pencil costs 30 naira less than a pen. Find the total cost of the pen and the pencil.
Cost of a pen = #x
Cost of a pencil = #(x - 30)
Cost of both = #x + #(x - 30)
= #x + #x - 30
= #2x - 30
Example: Find the sum of the whole number x and the next whole number above it.
First whole no: x
Next whole no above it: x + 1
Sum of the two: = x + x + 1
= 2x + 1.
A girl has x naira and her friend has #300 more than her. How much money do they have altogether?
Girl: = #x
Total: #x + #x + #300
= #( 2x + 300).
EVALUATION: The lesson is evaluated from New General Mathematics for JS1, Page 129, Ex. 15k,Questions 1 and 2.
ASSIGNMENT: Answer questions 4 and 7 from New General Mathematics 1, Page 129, Exercise 15k.
further studies
http://www.mathleague.com/help/algebra/algebra.htm
watch video
https://youtu.be/PIDnJAsRuZY
TOPIC: Removing Brackets.
REFERENCE BOOK: New General Mathematics f or JS1, Page 127.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to remove brackets from simple numerical and algebraic expressions.
CONTENTS
Positive sign before a bracket: When there is a positive sign before a bracket, the signs inside the bracket remain the same.
Simplify: 7g + (3g + 4h)
= 7g + 3g + 4h
= 10g + 4h.
Simplify: 13p + (6p - 3p)
= 13p + 6p - 3p
= 19p - 3p
= 16p.
Simplify: (6x - 5y) + (3y + 4x)
= 6x - 5y + 3y + 4x
= 6x + 4x +3y - 5y = 10x - 2y
EVALUATION: The lesson is evaluated from New General Mathematics for JS1, Page 127, Ex. 15g, Questions 9 -12.
ASSIGNMENT: Answer questions 13, 14 and 15 from new General Mathematics for JS1, Page 127 Ex. 15g.
further studies
http://www.mathsisfun.com/algebra/expanding.html
https://youtu.be/v-6MShC82ow
LESSON19
TOPIC: Removing brackets: Negative sign before a bracket.
REFERENCE BOOK: New General Mathematics for JS1, Page127.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to remove brackets from expressions having negative signs before the brackets.
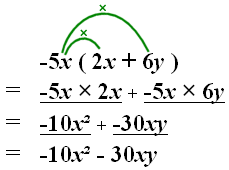
CONTENTS
Examples:
Simplify:
(a)
= 5a - (2a + 8 )
= 5a - 2a - 8
= 3a - 8.
In general, when there is a negative sign before a bracket: the signs of the terms inside the bracket are changed when the bracket is removed.
(b) Simplify:
10d - (9c - 4d)
= 10d - 9c + 4d
= 10d + 4d - 9c
= 14d - 9c.
(C ) Simplify:
(6x - y ) - (7x- 2y)
= 6x - y - 7x + 2y
= 6x - 7x + 2y - y
= -x + y or y - x .
EVALUATION: Remove brackets from the following and then simplify:
(a) 3a - (a + 5)
(b) 5x - (2 - x)
(c) (14x + 5y) - (7x - 6y)
(d) (8x + 3y)- (4x + y).
ASSIGNMENT: Answer questions 10 - 12 of exercise 15j, Page128 from New General Mathematics for JS1.
further studies
http://www.themathpage.com/alg/parentheses.htm
http://www.math-only-math.com/removal-of-brackets.html
https://youtu.be/LDIiYKYvvdA
LESSON 20
TOPIC: Algebraic Simplification: (Word Problems)
REFERENCE BOOK: New General Mathematics f or JS1, Page128.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve word problems on algebraic simplification.

CONTENTS
Example: A pen costs x naira and a pencil costs 30 naira less than a pen. Find the total cost of the pen and the pencil.
Cost of a pen = #x
Cost of a pencil = #(x - 30)
Cost of both = #x + #(x - 30)
= #x + #x - 30
= #2x - 30
Example: Find the sum of the whole number x and the next whole number above it.
First whole no: x
Next whole no above it: x + 1
Sum of the two: = x + x + 1
= 2x + 1.
A girl has x naira and her friend has #300 more than her. How much money do they have altogether?
Girl: = #x
Total: #x + #x + #300
= #( 2x + 300).
EVALUATION: The lesson is evaluated from New General Mathematics for JS1, Page 129, Ex. 15k,Questions 1 and 2.
ASSIGNMENT: Answer questions 4 and 7 from New General Mathematics 1, Page 129, Exercise 15k.
further studies
http://www.mathleague.com/help/algebra/algebra.htm
watch video
https://youtu.be/PIDnJAsRuZY
WEEK 9
LESSON 21
TOPIC: QUANTITATIVE REASONING ON THE USE OF BRACKETS
CONTENT:
Word problems on the use of brackets
Word problems in symbolic terms
A. Sample
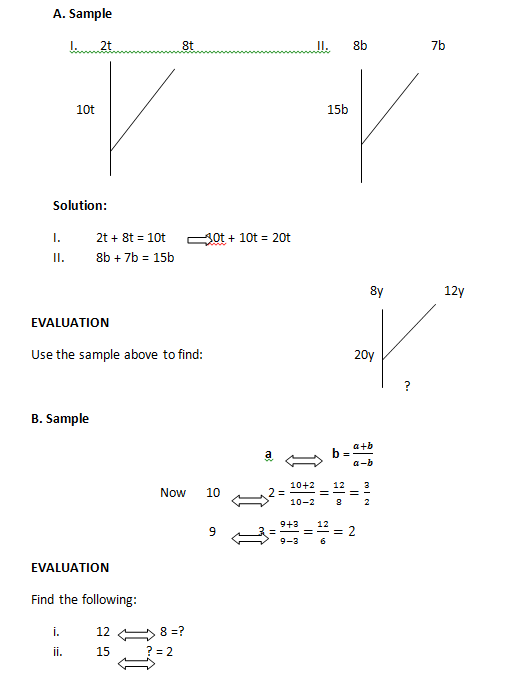
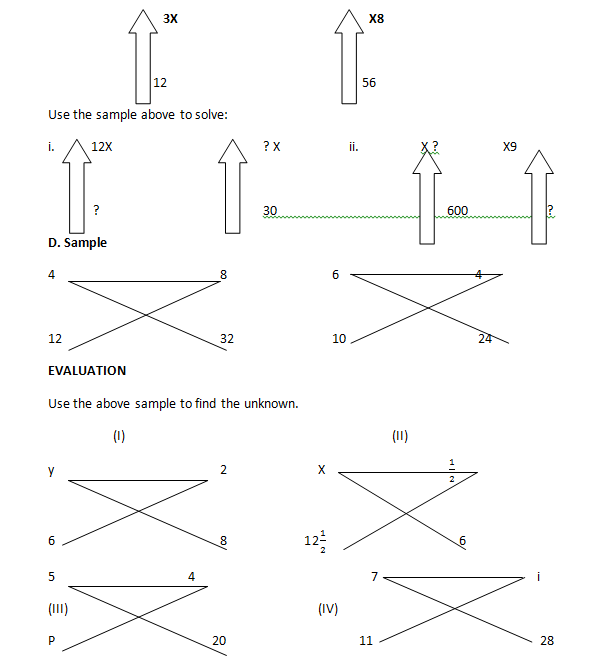
C. Sample
LESSON 22
TOPIC: SIMPLE EQUATIONS
CONTENT:
Translation of word problems into mathematical statements
Definition of simple equation
Use of sign of equality in mathematical statements
Solution of simple equations
TRANSLATION OF WORD PROBLEMS INTO MATHEMATICAL STATEMENTS
A sentence or statement says something about numbers written in symbols. Consider, for example the statement: “I think of a number, I then triple it and add 4 to it”. We proceed as follows to write the statement in symbols. Let the number thought of be “r”, tripling it gives “3r”, and by adding 4 we get “3r + 4”.
If the result of this process is 16, then we have 3r+ 4 = 16.
This symbolic expression is called a simple equation, with one unknown quantity, r. The expression contains two sides referred to as left hand side, 3r + 4, and the right hand side 16. The symbol ‘=’ is called the equality sign, which tells us that what is on the right-hand side is the same as what is on the left hand side.
Example 1:
Translate the following statements into mathematical algebraic equations.
I think of a number n, then subtract 4; the result is 10.
I think of a number x, then add 5; the result is 12.
I think of a number y; then double it, add 5, the result is 11.
Think of a certain number, divide it by 3 then double then add 12; the result is 18.
The sum of two consecutive whole numbers is 17. What are these numbers?
Solution
(a). n-4 = 10 (b).x + 5 = 12 (c).2y + 5 = 11(d) r/3+12=18 (e). n+(n+1)= 17
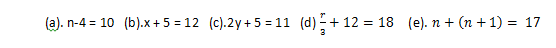
Evaluation:
Translate the following word sentences into mathematical statements:
One - third of a number is subtracted from half and the result is one.
5 is added to a number and the result is 9.
Two fifths of a number is added to 9 and the result is 12.
Example 2
Olu thinks of a number, 3 is added to it and the result is 8. What is the number?
Solution:
Let the number be x.
x + 3 = 8
subtract 3 from each side.
x+3 -3 = 8 – 3
x = 5
Evaluation:
Out of a certain number of sheep in a garden, 6 of them escaped leaving behind 117; how many sheep were in the garden originally?
Emeka added up his marks due to a mistake to get 25 marks; how many marks had he got at first?
https://youtu.be/N_8srGGX0kk
https://youtu.be/lV0DCdXJSHE
READING ASSIGNMENT:
New General Mathematics JSS 1 pg 40-43
ASSIGNMENT:
New General Mathematics JSS 1 pg 43
Exercise 5g: Q5-Q10.
TOPIC: QUANTITATIVE REASONING ON THE USE OF BRACKETS
CONTENT:
Word problems on the use of brackets
Word problems in symbolic terms
A. Sample

C. Sample

LESSON 22
TOPIC: SIMPLE EQUATIONS
CONTENT:
Translation of word problems into mathematical statements
Definition of simple equation
Use of sign of equality in mathematical statements
Solution of simple equations
TRANSLATION OF WORD PROBLEMS INTO MATHEMATICAL STATEMENTS
A sentence or statement says something about numbers written in symbols. Consider, for example the statement: “I think of a number, I then triple it and add 4 to it”. We proceed as follows to write the statement in symbols. Let the number thought of be “r”, tripling it gives “3r”, and by adding 4 we get “3r + 4”.
If the result of this process is 16, then we have 3r+ 4 = 16.
This symbolic expression is called a simple equation, with one unknown quantity, r. The expression contains two sides referred to as left hand side, 3r + 4, and the right hand side 16. The symbol ‘=’ is called the equality sign, which tells us that what is on the right-hand side is the same as what is on the left hand side.
Example 1:
Translate the following statements into mathematical algebraic equations.
I think of a number n, then subtract 4; the result is 10.
I think of a number x, then add 5; the result is 12.
I think of a number y; then double it, add 5, the result is 11.
Think of a certain number, divide it by 3 then double then add 12; the result is 18.
The sum of two consecutive whole numbers is 17. What are these numbers?
Solution
(a). n-4 = 10 (b).x + 5 = 12 (c).2y + 5 = 11(d) r/3+12=18 (e). n+(n+1)= 17
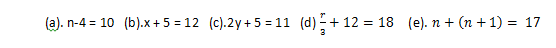
Evaluation:
Translate the following word sentences into mathematical statements:
One - third of a number is subtracted from half and the result is one.
5 is added to a number and the result is 9.
Two fifths of a number is added to 9 and the result is 12.
Example 2
Olu thinks of a number, 3 is added to it and the result is 8. What is the number?
Solution:
Let the number be x.
x + 3 = 8
subtract 3 from each side.
x+3 -3 = 8 – 3
x = 5
Evaluation:
Out of a certain number of sheep in a garden, 6 of them escaped leaving behind 117; how many sheep were in the garden originally?
Emeka added up his marks due to a mistake to get 25 marks; how many marks had he got at first?
https://youtu.be/N_8srGGX0kk
https://youtu.be/lV0DCdXJSHE
READING ASSIGNMENT:
New General Mathematics JSS 1 pg 40-43
ASSIGNMENT:
New General Mathematics JSS 1 pg 43
Exercise 5g: Q5-Q10.